问题提出：（1）同学们在探索求代数式x2+9+（15-x）2+25的最小值的过程时，老师进行了如下的引导，如图1，C为线段BD上的一个动点，分别过点B，D作AB⊥BD，ED⊥BD，连接AC，EC．已知AB=4，DE=1，BD=12，设CD=x.
①则AC+CE的长为 x2-24x+160+x2+1x2-24x+160+x2+1．（用含x的代数式表示）
②如图2，过A作AF⊥DE交ED的延长线于F，构造长方形ABDF，连接AE，此时A、C、E三点共线，AC+CE的值最小，求最小值．
问题解决：（2）请用上述的构图法求出代数式x2+9+（15-x）2+25的最小值．
x
2
+
9
（
15
-
x
）
2
+
25
x
2
-
24
x
+
160
+
x
2
+
1
x
2
-
24
x
+
160
+
x
2
+
1
x
2
+
9
（
15
-
x
）
2
+
25
【考点】轴对称-最短路线问题；矩形的性质．
【答案】
x
2
-
24
x
+
160
+
x
2
+
1
【解答】
【点评】
声明：本试题解析著作权属菁优网所有，未经书面同意，不得复制发布。
发布：2024/8/31 0:0:8组卷：435引用：4难度：0.5
相似题
-
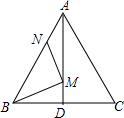1．如图，在等边△ABC中，AB=6，N为AB上一点，且AN=2，∠BAC的平分线交BC于点D，M是AD上的动点，连接BM，MN，则BM+MN的最小值是（ ）发布：2025/6/17 9:0:1组卷：1409引用：5难度：0.5 -
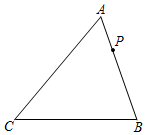2．如图，在锐角△ABC中，∠ACB=50°；边AB上有一定点P，M、N分别是AC和BC边上的动点，当△PMN的周长最小时，∠MPN的度数是（ ）发布：2025/6/17 7:0:2组卷：3992引用：15难度：0.5 -
3．如图1，菱形ABCD的对角线AC、BD相交于点O，且AC=6cm,BD=8cm,分别过点B、C作AC与BD的平行线相交于点E．
（1）判断四边形BOCE的形状并证明；
（2）点G从点A沿射线AC的方向以2cm/s的速度移动了t秒，连接BG，当S△ABG=2S△OBG时，求t的值．
（3）如图2，长度为3cm的线段GH在射线AC上运动，求BG+BH的最小值．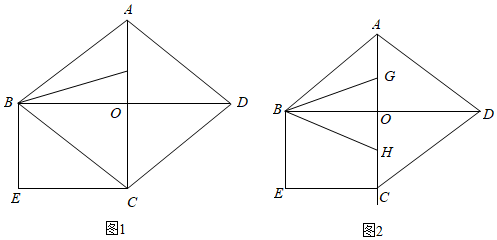
发布：2025/6/17 8:0:1组卷：899引用：2难度：0.2
