如图，正方形ABCD中，AC是对角线，今有较大的直角三角板，一边始终经过点B，直角顶点P在射线AC上移动，另一边交DC于Q．
（1）如图1，当点Q在DC边上时，探究PB与PQ所满足的数量关系；
小明同学探究此问题的方法是：
过P点作PE⊥DC于E点，PF⊥BC于F点，
根据正方形的性质和角平分线的性质，得出PE=PF，
再证明△PEQ≌△PFB，可得出结论，他的结论应是PB=PQPB=PQ；
（2）如图2，当点Q落在DC的延长线上时，猜想并写出PB与PQ满足的数量关系，并证明你的猜想．
【答案】PB=PQ
【解答】
【点评】
声明：本试题解析著作权属菁优网所有，未经书面同意，不得复制发布。
发布：2024/7/6 8:0:9组卷：1584引用：3难度：0.3
相似题
-
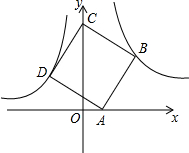1．如图，点B（3，3）在双曲线y=（x＞0）上，点D在双曲线y=-kx（x＜0）上，点A和点C分别在x轴，y轴的正半轴上，且点A，B，C，D构成的四边形为正方形．4x
（1）求k的值；
（2）求点A的坐标．发布：2025/6/17 20:30:2组卷：2119引用：79难度：0.5 -
2．如图，E、F分别是正方形ABCD的边CD，AD上的点，且CE=DF，AE，BF相交于点O，下列结论①AE=BF；②AE⊥BF；③AO=OE；④S△AOB=S四边形DEOF中，正确结论的个数为（ ）发布：2025/6/17 15:30:1组卷：3091引用：25难度：0.7 -
3．如图，正方形ABCD的对角线AC，BD相交于点O，那么图中共有 个等腰直角三角形．发布：2025/6/17 20:0:2组卷：147引用：22难度：0.5
