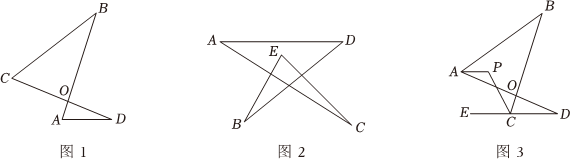
如图1，线段AB，CD相交于点O，连接AD，CB，我们把形如图1的图形称为“8字形”．
（1）求证：∠A+∠D=∠B+∠C；
（2）如图2，求∠A+∠B+∠C+∠D+∠E的度数；
（3）如图3，AP平分∠BAD，CP平分∠BCD的邻补角∠BCE，试猜想∠P，∠D与∠B之间的数量关系，并说明理由．
【考点】三角形内角和定理．
【答案】（1）证明见解析；
（2）180°；
（3）2∠P-∠D-∠B=180°．
（2）180°；
（3）2∠P-∠D-∠B=180°．
【解答】
【点评】
声明：本试题解析著作权属菁优网所有，未经书面同意，不得复制发布。
发布：2024/9/20 13:0:8组卷：195引用：1难度：0.5
相似题
-
1．△ABC中，AB、AC边的高线交于点O，∠A=50°，则∠BOC=．
发布：2025/6/17 19:0:1组卷：34引用：1难度：0.4 -
2．如图①，在△ABC中，AE平分∠BAC，交BC于点E，∠C＞∠B，且FD⊥BC于点D．
（1）试推出∠EFD，∠B，∠C的关系；
（2）如图②，当点F在AE的延长线上时，其余条件不变，（1）中的结论还成立吗？请说明理由．
发布：2025/6/17 21:30:1组卷：155引用：1难度：0.5 -
3．如图，△ABC中，BD、BE分别是高和角平分线，点F在CA的延长线上，FH⊥BE，交BD于点G，交BC于点H．下列结论：①∠DBE=∠F； ②2∠BEF=∠BAF+∠C；③∠F=∠BAC-∠C；④∠BGH=∠ABE+∠C．其中正确个数是（ ）发布：2025/6/17 21:30:1组卷：1883引用：10难度：0.5
