某果园种植“糖心苹果”已有十余年,为了提高利润,该果园每年投入一定的资金,对种植、采摘、包装、宣传等环节进行改进.如图是2013年至2022年,该果园每年的投资金额x(单位:万元)与年利润增量y(单位:万元)的散点图:

该果园为了预测2023年投资金额为20万元时的年利润增量,建立了y关于x的两个回归模型;
模型①:由最小二乘公式可求得y与x的线性回归方程:̂y=2.50x-2.50;
模型②:由图中样本点的分布,可以认为样本点集中在曲线:y=blnx+a的附近,对投资金额x做交换,令t=lnx,则y=b•t+a,且有10∑i=1ti=22.00,10∑i=1yi=230,10∑i=1tiyi=569.00,10∑i=1ti2=50.92.
(1)根据所给的统计量,求模型②中y关于x的回归方程;
(2)根据下列表格中的数据,比较两种模型的相关指数R2,并选择拟合精度更高、更可靠的模型,预测投资金额为20万元时的年利润增量(结果保留两位小数).
̂
y
=
2
.
50
x
-
2
.
50
10
∑
i
=
1
t
i
=
22
.
00
10
∑
i
=
1
y
i
=
230
10
∑
i
=
1
t
i
y
i
=
569
.
00
10
∑
i
=
1
t
i
2
=
50
.
92
| 回归模型 | 模型① | 模型② |
| 回归方程 | ̂ y = 2 . 50 x - 2 . 50 |
̂ y = blnx + a |
10 ∑ i = 1 ( y i - ̂ y i ) 2 |
102.28 | 36.19 |
̂
b
=
n
∑
i
=
1
(
t
i
-
t
)
(
y
i
-
y
)
n
∑
i
=
1
(
t
i
-
t
)
2
̂
a
=
y
-
̂
b
t
相关指数
R
2
=
1
-
n
∑
i
=
1
(
y
i
-
̂
y
)
2
n
∑
i
=
1
(
y
i
-
y
)
2
参考数据:ln2≈0.6931,ln5≈1.6094.
【考点】经验回归方程与经验回归直线.
【答案】(1);
(2)模型①的R2小于模型②,选择模型②;42.89(万元).
̂
y
=
25
lnx
-
32
(2)模型①的R2小于模型②,选择模型②;42.89(万元).
【解答】
【点评】
声明:本试题解析著作权属菁优网所有,未经书面同意,不得复制发布。
发布:2024/7/11 8:0:9组卷:31引用:3难度:0.6
相似题
-
 1.某科研机构为了了解气温对蘑菇产量的影响,随机抽取了某蘑菇种植大棚12月份中5天的日产量y(单位:kg)与该地当日的平均气温x(单位:℃)的数据,得到如图散点图:
1.某科研机构为了了解气温对蘑菇产量的影响,随机抽取了某蘑菇种植大棚12月份中5天的日产量y(单位:kg)与该地当日的平均气温x(单位:℃)的数据,得到如图散点图:
其中A(3,2),B(5,10),C(8,11),D(9,13),E(10,14).
(1)求出y关于x的线性回归方程;
(2)若该地12月份某天的平均气温为6℃,用(1)中所求的回归方程预测该蘑菇种植大棚当日的产量.
附:线性回归直线方程中,̂y=̂bx+̂a,̂b=n∑i=1xiyi-nxyn∑i=1x2i-nx2.̂a=y-̂bx发布:2024/12/29 11:30:2组卷:104引用:3难度:0.7 -
2.两个线性相关变量x与y的统计数据如表:
其回归直线方程是x 9 9.5 10 10.5 11 y 11 10 8 6 5 =̂yx+40,则相应于点(9,11)的残差为 .̂b发布:2024/12/29 12:0:2组卷:116引用:8难度:0.7 -
3.某农科所对冬季昼夜温差(最高温度与最低温度的差)大小与某反季节大豆新品种一天内发芽数之间的关系进行了分析研究,他们分别记录了12月1日至12月6日每天昼夜最高、最低的温度(如图1),以及实验室每天每100颗种子中的发芽数情况(如图2),得到如下资料:
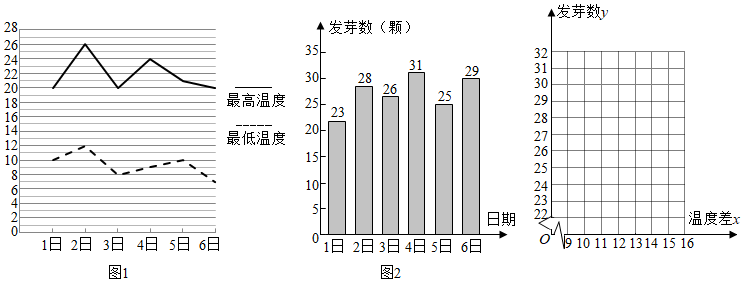
(1)请画出发芽数y与温差x的散点图;
(2)若建立发芽数y与温差x之间的线性回归模型,请用相关系数说明建立模型的合理性;
(3)①求出发芽数y与温差x之间的回归方程(系数精确到0.01);̂y=̂a+̂bx
②若12月7日的昼夜温差为8℃,通过建立的y关于x的回归方程,估计该实验室12月7日当天100颗种子的发芽数.
参考数据:=2051,6∑i=1xi=75,6∑i=1yi=162,6∑i=1xiyi≈4.2,6∑i=1xi2-6x2≈6.5.6∑i=1yi2-6y2
参考公式:
相关系数:r=(当|r|>0.75时,具有较强的相关关系).n∑i=1xiyi-nx•y(n∑i=1xi2-nx2)(n∑i=1yi2-ny2)
回归方程中斜率和截距计算公式:̂y=̂a+̂bx=̂b,n∑i=1xiyi-nx•yn∑i=1xi2-nx2=̂ay-̂b.x发布:2024/12/29 12:0:2组卷:189引用:5难度:0.5


