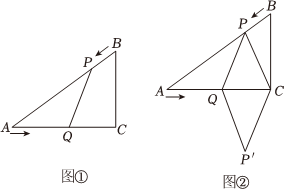
综合与探究：已知：如图①，在Rt△ABC中，∠C=90°，AC=8cm,BC=6cm,点P由B出发沿BA方向向点A匀速运动，速度为1cm/s；点Q由A出发沿AC方向向点C匀速运动，速度为2cm/s；连接PQ．若设运动的时间为t（s）（0＜t＜4），解答下列问题：
（1）当AP=AQ时，求t的值；
（2）点P，Q同时出发，t为何值时，以A，P，Q为顶点的三角形与△ABC相似；
（3）如图②，连接PC，并把△PQC沿QC翻折，得到四边形PQP'C，那么是否存在某一时刻t,使四边形PQP'C为菱形？若存在，直接写出此时t的值；若不存在，说明理由．（不写求解过程）
【考点】相似形综合题．
【答案】（1）；
（2）或；
（3）存在某一时刻t，使四边形PQP'C为菱形，．
10
3
（2）
20
7
50
13
（3）存在某一时刻t，使四边形PQP'C为菱形，
t
=
20
9
【解答】
【点评】
声明：本试题解析著作权属菁优网所有，未经书面同意，不得复制发布。
发布：2024/9/24 1:0:8组卷：87引用：3难度：0.2
相似题
-
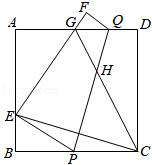1．如图，将正方形纸片ABCD沿PQ折叠，使点C的对称点E落在边AB上，点D的对称点为点F，EF交AD于点G，连接CG交PQ于点H，连接CE，EH．
（1）求证：△PBE∽△QFG；
（2）求∠ECG的度数；
（3）求证：EG2-CH2=GQ•GD．发布：2025/5/25 21:0:1组卷：400引用：2难度：0.3 -
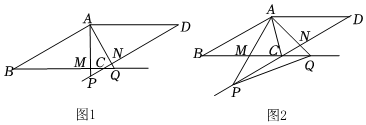2．如图1，在菱形ABCD中，∠ABC是锐角，P、Q分别是边DC、BC延长线上的动点，连接AP、AQ分别交BC、DC于点M、N．
（1）当AP⊥BC且∠PAQ=∠D时，证明：△ABM≌△ADN；
（2）如图2，当∠PAQ=∠BCD时，连接AC、PQ．12
①证明：AC2=CP•CQ；
②若AB=4，AC=2，则当CM为何值时，△APQ是以PQ为底边的等腰三角形．发布：2025/5/25 21:30:1组卷：184引用：1难度：0.1 -
3．【证明体验】（1）如图1，△ABC中，D为BC边上任意一点，作DE⊥AC于E，若∠CDE=
∠A，求证：△ABC为等腰三角形；12
【尝试应用】
（2）如图2，四边形ABCD中，∠D=90°，AD=CD，AE平分∠BAD，∠BCD+∠EAD=180°，若DE=2，AB=6，求AE的长；
【拓展延伸】
（3）如图3，△ABC中，点D在AB边上满足CD=BD，∠ACB=90°+∠B，若AC=1012，BC=20，求AD的长．3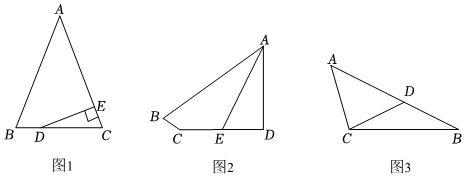
发布：2025/5/25 20:0:1组卷：497引用：1难度：0.3
