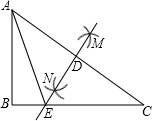
如图，在Rt△ABC中，∠B=90°，分别以A、C为圆心，大于AC长的一半为半径画弧，两弧相交于点M、N，连接MN，与AC、BC分别相交于点D、E，连接AE，当AB=3，AC=5时，△ABE周长为（ ）
【考点】作图—基本作图；线段垂直平分线的性质．
【答案】A
【解答】
【点评】
声明：本试题解析著作权属菁优网所有，未经书面同意，不得复制发布。
发布：2024/8/26 10:0:8组卷：308引用：5难度：0.7
相似题
-
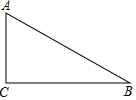1．如图，在Rt△ABC中，∠ACB=90°．
（1）用直尺和圆规作∠BAC的平分线交BC于D（保留痕迹）；
（2）若AD=DB，求∠B的度数．发布：2025/5/24 18:30:1组卷：423引用：16难度：0.7 -
2．如图，已知∠AOB，用直尺和圆规按照以下步骤作图：
①以点O为圆心，任意长为半径画弧，分别交OA、OB于点C、D；
②画射线O′A'，以点O'为圆心，OC长为半径画弧，交O′A'于点C'；
③以点C′为圆心，CD长为半径画弧，与第②步中所画的弧相交于点D'；
④过点D′画射线O′B'；
根据以上操作，可以判定△OCD≌△O'C'D'，其判定的依据是（ ）
发布：2025/5/24 19:30:1组卷：499引用：7难度：0.5 -
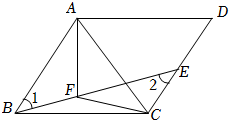3．如图，在▱ABCD中，E为CD边上一点，连接BE，F为BE上一点，且BF=CE，EF=CD．连接AC、AF、CF．
（1）用尺规完成以下基本作图：作∠AFC的角平分线交AC于点G；（保留作图痕迹，不写作法，不下结论）
（2）求证：FG⊥AC．
请将下列证明过程补充完整：
证明：∵四边形ABCD是平行四边形，
∴AB∥CD，AB=CD．
∵AB=CD，EF=CD，
∴①．
∵AB∥CD，
∴②．
又∵③．
∴△ABF≌△FEC（SAS）．
∴④．
∵FG平分∠AFC，
∴FG⊥AC．发布：2025/5/24 18:0:1组卷：185引用：2难度：0.5
