正四面体的顶点数和棱数分别是( )
【考点】欧拉公式.
【答案】D
【解答】
【点评】
声明:本试题解析著作权属菁优网所有,未经书面同意,不得复制发布。
发布:2024/5/27 14:0:0组卷:107引用:2难度:0.9
相似题
-
1.一个棱柱有18条棱,那么它的底面一定是( )
发布:2025/6/14 4:0:2组卷:996引用:35难度:0.9 -
2.十八世纪瑞士数学家欧拉证明了简单多面体中顶点数(V)、面数(F)、棱数(E)之间存在的一个有趣的关系式,被称为欧拉公式.请你观察如图几种简单多面体模型,解答下列问题:
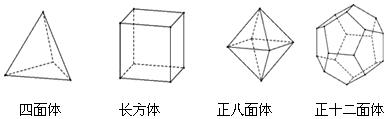
(1)根据上面多面体模型,完成表格中的空格:
你发现顶点数(V)、面数(F)、棱数(F)之间存在的关系式是 .多面体 顶点数(V) 面数(F) 棱数(E) 四面体 长方体 正八面体 正十二面体
(2)一个多面体的面数比顶点数小8,且有30条棱,则这多面体的顶点数是 ;
(3)某个玻璃饰品的外形是简单多面体,它的外表是由三角形和八边形两种多边形拼接而成,且有48个顶点,每个顶点处都有3条棱,设该多面体表面三角形的个数为x个,八边形的个数为y个,求x+y的值.发布:2025/6/16 18:30:2组卷:180引用:1难度:0.4 -
3.正多面体共有五种,它们是 、、、、,它们的面数f,棱数e、顶点数v满足关系式 .
发布:2025/5/28 2:0:5组卷:67引用:1难度:0.5


