在平面直角坐标系中，反比例函数y=kx（k＞0）的图象与一次函数y=mx+b（m＜0）的图象在第一象限交于A、B两点．
探究一：
P是平面内的一点，过点A、B、P分别作x轴、y轴的垂线，相应的两条垂线与坐标轴所围成的矩形面积记为SA、SB、SP，矩形周长记为CA、CB、CP．
（1）如图1，P是线段AB上不与点A、B重合的一点，k=8．
SA=88，SA＜＜SP（填“＞”、“＜”或“=”）；
猜想：当点P从点A运动到点B时，SP的变化规律是 先变大后变小先变大后变小；
（2）如图2，P是双曲线AB段上不与点A、B重合的一点，m=-1，b=4．
CA=88，CA＞＞CP．（填“＞”、“＜”或“=”）；
猜想：当点P从点A运动到点B时，CP的变化规律是 先变小后变大先变小后变大．
探究二：
如图3，过点A作x轴的垂线，过点B作y轴的垂线，两条垂线交于直线AB右上方的点Q，OQ与反比例函数的图象交于点G．若G是OQ的中点，且△QAB的面积为9，求k的值．
y
=
k
x
（
k
＞
0
）
【考点】反比例函数综合题．
【答案】8；＜；先变大后变小；8；＞；先变小后变大
【解答】
【点评】
声明：本试题解析著作权属菁优网所有，未经书面同意，不得复制发布。
发布：2024/6/8 8:0:9组卷：578引用：1难度：0.2
相似题
-
1．如图1，点P为∠MON的平分线上一点，以P为顶点的角的两边分别与射线OM，ON交于A，B两点，如果∠APB绕点P旋转时始终满足OA•OB=OP2，我们就把∠APB叫做∠MON的智慧角．
（1）如图2，已知∠MON=90°，点P为∠MON的平分线上一点，以P为顶点的角的两边分别与射线OM，ON交于A，B两点，且∠APB=135°．求证：∠APB是∠MON的智慧角．
（2）如图1，已知∠MON=α（0°＜α＜90°），OP=2．若∠APB是∠MON的智慧角，连接AB，用含α的式子分别表示∠APB的度数和△AOB的面积．
（3）如图3，C是函数y=（x＞0）图象上的一个动点，过C的直线CD分别交x轴和y轴于A，B两点，且满足BC=2CA，请求出∠AOB的智慧角∠APB的顶点P的坐标．3x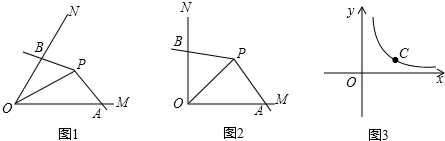
发布：2025/6/25 6:0:1组卷：3770引用：51难度：0.5 -
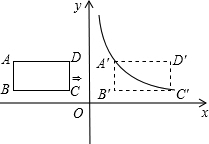2．如图，在平面直角坐标系中，四边形ABCD是矩形，AD∥x轴，A（-3，），AB=1，AD=2．32
（1）直接写出B、C、D三点的坐标；
（2）将矩形ABCD向右平移m个单位，使点A、C恰好同时落在反比例函数y=（x＞0）的图象上，得矩形A′B′C′D′．求矩形ABCD的平移距离m和反比例函数的解析式．kx发布：2025/6/25 6:0:1组卷：1948引用：59难度：0.5 -
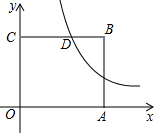3．如图，在平面直角坐标系中，点O为坐标原点，正方形OABC的边OA、OC分别在x轴、y轴上，点B的坐标为（2，2），反比例函数（x＞0，k≠0）的图象经过线段BC的中点D．y=kx
（1）求k的值；
（2）若点P（x,y）在该反比例函数的图象上运动（不与点D重合），过点P作PR⊥y轴于点R，作PQ⊥BC所在直线于点Q，记四边形CQPR的面积为S，求S关于x的解析式并写出x的取值范围．发布：2025/6/25 6:0:1组卷：1664引用：56难度：0.5
