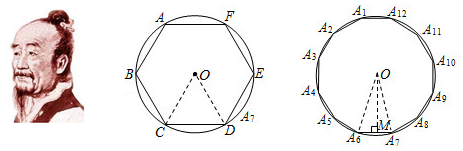
我国魏晋时期的数学家刘徽首创“割圆术”：“割之弥细，所失弥少，割之又割，以至于不可割，则与圆周合体，而无所失矣”，即通过圆内接正多边形割圆，从正六边形开始，每次边数成倍增加，依次可得圆内接正十二边形，内接正二十四边形，…．边数越多割得越细，正多边形的周长就越接近圆的周长．再根据“圆周率等于圆周长与该圆直径的比”来计算圆周率．设圆的半径为R，图1中圆内接正六边形的周长l6=6R，则π≈l62R=3．再利用圆的内接正十二边形来计算圆周率，则圆周率π约为（ ）
l
6
2
R
【答案】A
【解答】
【点评】
声明：本试题解析著作权属菁优网所有，未经书面同意，不得复制发布。
发布：2024/5/27 14:0:0组卷：1124引用：8难度：0.5
相似题
-
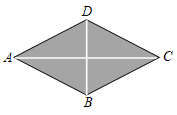1．如图，菱形花坛ABCD的周长为80m,∠BAD=60°，沿着菱形的对角线修建两条小路AC和BD，则小路BD的长是（ ）发布：2025/6/10 16:30:2组卷：254引用：2难度：0.9 -
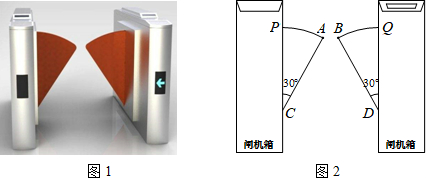
2．图1是一个地铁站入口的双翼闸机．如图2，它的双翼展开时，双翼边缘的端点A与B之间的距离为10cm,双翼的边缘AC=BD=54cm,且与闸机侧立面夹角∠PCA=∠BDQ=30°．当双翼收起时，可以通过闸机的物体的最大宽度为（ ）
发布：2025/6/10 17:0:2组卷：3590引用：48难度：0.6 -
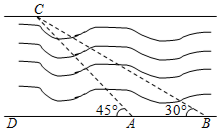3．如图，同学们利用所学知识去测量三江源某河段某处的宽度，小明同学在A处观测对岸点C．测得∠CAD=45°，小刚同学在距点A处60米远的B点测得∠CBD=30°，根据这些数据可以算出河宽为 米（精确到0.01米，≈1.414，2≈1.732）．3发布：2025/6/10 17:30:1组卷：467引用：4难度：0.5
