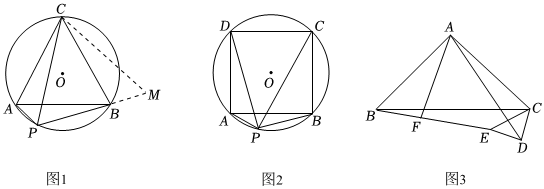
问题提出：如图1所示，等边△ABC内接于⊙O，点P是ˆAB上的任意一点，连接PA，PB，PC．线段PA，PB，PC满足怎样的数量关系？
（1）尝试解决：为了解决这个问题，小明给出这种解题思路：由条件CA=CB，∠ACB=60°，从而将CP绕点C逆时针旋转60°交PB延长线于点M，从而证明△PAC≌△MBC，请你完成余下思考，并直接写出答案：PA，PB，PC的数量关系是 PC=PA+PBPC=PA+PB；
（2）自主探索：如图2所示，把原问题中的“等边△ABC”改成“正方形ABCD”，其余条件不变，
①PC与PA，PB有怎样的数量关系？请说明理由；
②PC+PD与PA，PB的数量关系是 PC+PD=（2+1）（PA+PB）PC+PD=（2+1）（PA+PB）.（直接写出结果）
（3）学以致用：如图3所示，在Rt△ABC中，∠BAC=90°，AB=AC=8，BE=45，连接CE，以CE为底作等腰直角三角形CDE，F是BE边上的一点，连接AD和AF，且∠FAD=45°，则BF的长为 2525．
ˆ
AB
2
+
1
2
+
1
BE
=
4
5
5
5
【考点】圆的综合题．
【答案】PC=PA+PB；PC+PD=（）（PA+PB）；2
2
+
1
5
【解答】
【点评】
声明：本试题解析著作权属菁优网所有，未经书面同意，不得复制发布。
发布：2024/10/12 3:0:1组卷：154引用：1难度：0.2
相似题
-
1．如图，AB是圆O的直径，弦CD⊥AB于G，射线DO与直线CE相交于点E，直线DB与CE交于点H，且∠BDC=∠BCH．
（1）求证：直线CE是圆O的切线．
（2）如图1，若OG=BG，BH=1，直接写出圆O的半径；
（3）如图2，在（2）的条件下，将射线DO绕D点逆时针旋转，得射线DM，DM与AB交于点M，与圆O及切线CF分别相交于点N，F，当GM=GD时，求切线CF的长．
发布：2025/1/28 8:0:2组卷：782引用：2难度：0.1 -
2．如图，AB是圆O的直径，AB=6，D是半圆ADB上的一点，C是弧BD的中点．
（1）若∠ABD=30°，求BC的长和由弦BC、BD、和弧CD围成的图形面积；
（2）若弧AD的度数是120度，在半径OB上是否存在点P，使得PC+PD的值最小，如果存在，请在备用图中画出P的位置，并求PC+PD的最小值，如果不存在，请说明理由．
发布：2025/1/28 8:0:2组卷：44引用：0难度：0.3 -
3．如图，AB是圆O的直径，弦CD与AB交于点H，∠BDC=∠CBE．
（1）求证：BE是圆O的切线；
（2）若CD⊥AB，AC=2，BH=3，求劣弧BC的长；
（3）如图，若CD∥BE，作DF∥BC，满足BC=2DF，连接FH、BF，求证：FH=BF．发布：2025/1/28 8:0:2组卷：100引用：1难度：0.1
