如图,抛物线C:y=ax2+bx+c(a≠0)的对称轴为直线x=-12,且抛物线经过A(-2,0),B(0,2)两点,交x轴于另一点C.
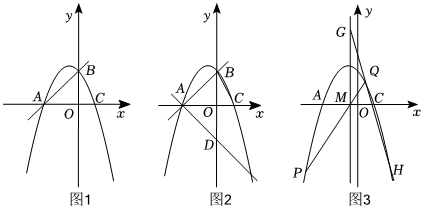
(1)求抛物线的解析式;
(2)过点A作直线AB的垂线交y轴于点D,平移直线AD交抛物线于点E,F两点,连结EO,FO.若△EFO为以EF为斜边的直角三角形,求平移后的直线的解析式.
(3)设对称轴直线x=-12与x轴交于M,点P为抛物线上对称轴左侧一点,直线PM交抛物线于另一点Q,点P关于抛物线对称轴对称点H,直线HQ交抛物线对称轴于G点,在点P运动过程中GM长是否为一定值,若为定值,请求出其值,若不为定值,请求出其变化范围.
x
=
-
1
2
x
=
-
1
2
【考点】二次函数的性质与图象.
【答案】(1)y=-x2-x+2;
(2)或;
(3)是,.
(2)
y
=
-
x
-
1
+
5
y
=
-
x
-
1
-
5
(3)是,
GM
=
9
2
【解答】
【点评】
声明:本试题解析著作权属菁优网所有,未经书面同意,不得复制发布。
发布:2024/5/31 8:0:9组卷:20引用:2难度:0.4
相似题
-
1.方程ay=b2x2+c中的a,b,c∈{-3,-2,0,1,2,3},且a,b,c互不相同,在所有这些方程所表示的曲线中,不同的抛物线共有条.
发布:2024/12/29 11:30:2组卷:95引用:5难度:0.5 -
2.园林工人计划使用可以做出20m栅栏的材料,在靠墙的位置围出一块矩形的花圃.要使得花圃的面积不小于42m2,你能确定与墙平行的栅栏的长度范围吗?
发布:2025/1/2 18:30:1组卷:17引用:9难度:0.8 -
3.园林工人计划使用可以做出20m栅栏的材料,在靠墙的位置围出一块矩形的花圃.要使得花圃的面积不小于42m2,你能确定与墙平行的栅栏的长度范围吗?
发布:2025/1/2 18:30:1组卷:3引用:1难度:0.5


