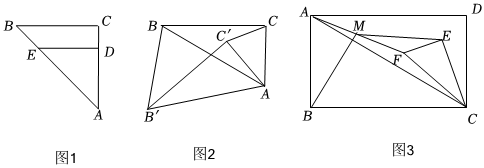
【初步发现】如图1，在Rt△ABC中，∠ACB=90°，AC=BC．点D，E分别在边AC，AB上，且DE∥BC，则CDBE=2222．
【探究证明】如图2，在Rt△ABC中，∠ACB=90°，∠ABC=30°．将△ACB绕点A旋转一定的角度后的图形是△AC′B′，连接CC′，BB′，求CC′BB′的值．
【综合拓展】如图3，在矩形ABCD中，∠ACB=∠FCE=30°，∠FEC=90°，M为AF的中点，求证：MB=ME．
CD
BE
2
2
2
2
CC
′
BB
′
【考点】相似形综合题．
【答案】
2
2
【解答】
【点评】
声明：本试题解析著作权属菁优网所有，未经书面同意，不得复制发布。
发布：2024/6/30 8:0:9组卷：95引用：1难度：0.1
相似题
-
1．综合与实践
问题情境：如图，在Rt△ABC中，∠ACB=90°，将△ABC绕点B顺时针旋转得到Rt△EBD，连接AE，连接CD并延长交AE于点F．
猜想验证：（1）试猜想△CBD与△ABE是否相似？并证明你的猜想．
探究证明：（2）如图，连接BF交DE于点H，AB与CF相交于点G，是否成立？并说明理由．DHBH=FHEH
拓展延伸：（3）若CD=EF，直接写出的值．BCAB发布：2025/5/23 21:30:2组卷：282引用：3难度：0.2 -
2．【实践操作】：
第一步：如图①，将矩形纸片ABCD沿过点D的直线折叠，使点A落在CD上的A'处，得到折痕DE，然后把纸片展平．
第二步：如图②，将图中的矩形纸片ABCD沿过点E的直线折叠，点C恰好落在AD上的点C'处，点B落在B'处，得到折痕EF，B'C'交AB于点M，C'F交DE于点N，再把纸片展平．
【问题解决】：
（1）如图①，四边形AEA'D的形状是 ；
（2）如图②，线段MC'与ME是否相等？若相等，请给出证明；若不相等，请说明理由；
（3）如图②，若AC'=3cm,DC'=6cm,则MC'=，=．DNEN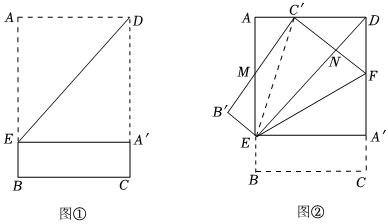
发布：2025/5/23 19:0:2组卷：311引用：3难度：0.1 -
3．如图，在矩形ABCD中，点M、N分别为AD、BC上的点，将矩形ABCD沿MN折叠，使点B落在CD边上的点E处（不与点C，D重合），连接BE，过点M作MH⊥BC于点H．
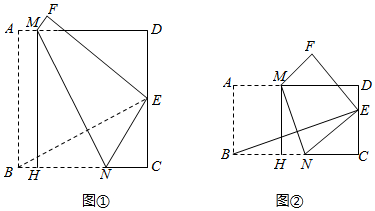
（1）如图①，若BC=AB，求证：△EBC≌△NMH；
（2）如图②，当BC=2AB时，
①求证：△EBC∽△NMH；
②若点E为CD的三等分点，请直接写出的值．AMBN发布：2025/5/23 20:30:1组卷：409引用：2难度：0.2
