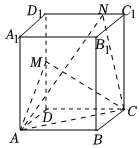
如图所示，四棱柱ABCD-A1B1C1D1的棱长均为2，侧棱与底面垂直，且∠BAD=60°，M是侧棱DD1的中点，N是直线C1D1上的点．
（Ⅰ）若以D为坐标原点，以DC为y轴的正方向，以DD1为z轴的正方向，建立空间（右手）直角坐标系，请写出点B1的坐标；
（Ⅱ）若二面角M-AC-N的平面角的余弦值为1010，试确定点N的位置．
DC
D
D
1
10
10
【考点】二面角的平面角及求法．
【答案】（Ⅰ）点B1的坐标为．
（Ⅱ）当点N位置在D1C1的延长线上且与点C1的距离等于2时，满足题设条件．
（
3
，
1
，
2
）
（Ⅱ）当点N位置在D1C1的延长线上且与点C1的距离等于2时，满足题设条件．
【解答】
【点评】
声明：本试题解析著作权属菁优网所有，未经书面同意，不得复制发布。
发布：2024/9/2 5:0:8组卷：39引用：2难度：0.4
相似题
-
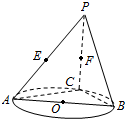1．如图，AB是圆O的直径，点C是圆O上异于A，B的点，直线PC⊥平面ABC，E，F分别是PA，PC的中点．
（Ⅰ）记平面BEF与平面ABC的交线为l,试判断直线l与平面PAC的位置关系，并加以证明；
（Ⅱ）设（Ⅰ）中的直线l与圆O的另一个交点为D，且点Q满足．记直线PQ与平面ABC所成的角为θ，异面直线PQ与EF所成的角为α，二面角E-l-C的大小为β．求证：sinθ=sinαsinβ．DQ=12CP发布：2025/1/20 8:0:1组卷：907引用：12难度：0.1 -
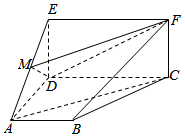2．如图，四边形ABCD为梯形，四边形CDEF为矩形，平面ABCD⊥平面CDEF，∠BAD=∠ADC=90°，AB=AD=DE=CD，M为AE的中点．12
（1）证明：AC∥平面MDF；
（2）求平面MDF与平面BCF的夹角的大小．发布：2025/1/2 8:0:1组卷：141引用：1难度：0.6 -
3．如图，AB是圆O的直径，PA垂直于圆所在的平面，C是圆周上的点．
（1）求证：平面PAC⊥平面PBC；
（2）若AB=2，AC=2，PA=2，求二面角C-PB-A的度数．2发布：2025/1/28 8:0:2组卷：33引用：1难度：0.5
