截长补短法在初中数学中有着重要的作用，它主要是用来证线段的和差问题．截长就是在较长的线段上截取一段等于要证的两段较短的线段中的一段．证剩下的那一段等于另外一段较短的线段．已知点O是线段AB垂直平分线l上的一个动点，以BO为边作等边△BOC，点C在直线AB的上方且在直线l的右侧，连接AC交直线l于点D，连接BD．
（1）如图1，点O在线段AB上，请直接用等式表示线段OD，BD，CD之间的数量关系：BD=OD+CDBD=OD+CD；
（2）若点O在线段AB的上方，连接AO，且满足∠ABO≠30°．如图2，当∠ABO＜30°时，请探究线段OD，BD，CD之间的数量关系，并说明理由．
【答案】BD=OD+CD
【解答】
【点评】
声明：本试题解析著作权属菁优网所有，未经书面同意，不得复制发布。
发布：2024/7/18 8:0:9组卷：309引用：2难度：0.5
相似题
-
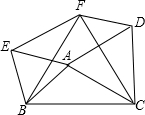1．如图，以△ABC的三边为边分别作等边△ACD、△ABE、△BCF，则下列结论：①△EBF≌△DFC；②四边形AEFD为平行四边形；③当AB=AC，∠BAC=120°时，四边形AEFD是正方形．其中正确的结论是．（请写出正确结论的序号）．发布：2025/6/22 21:30:2组卷：2346引用：61难度：0.5 -
2．直线CD经过∠BCA的顶点C，CA=CB．E、F分别是直线CD上两点，且∠BEC=∠CFA=∠α．
（1）若直线CD经过∠BCA的内部，且E、F在射线CD上，请解决下面两个问题：
①如图1，若∠BCA=90°，∠α=90°，则EF |BE-AF|（填“＞”，“＜”或“=”号）；
②如图2，若0°＜∠BCA＜180°，若使①中的结论仍然成立，则∠α与∠BCA应满足的关系是 ；
（2）如图3，若直线CD经过∠BCA的外部，∠α=∠BCA，请探究EF、与BE、AF三条线段的数量关系，并给予证明．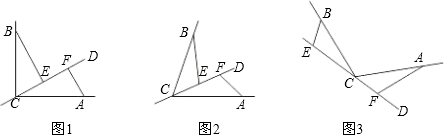
发布：2025/6/22 21:0:10组卷：857引用：10难度：0.5 -
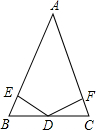3．已知：如图，在△ABC中，AB=AC，D是BC的中点，DE⊥AB，DF⊥AC，E，F分别是垂足，求证：AE=AF．发布：2025/6/22 22:0:2组卷：134引用：11难度：0.7
