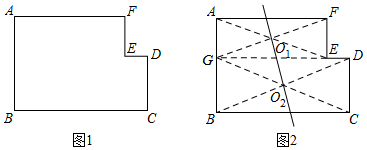
如图1，∠A=∠B=∠C=∠D=∠E=∠F=90°，AB，FE，DC为铅直方向的边，AF，ED，BC为水平方向的边，点E在AB，CD之间，且在AF，BC之间，我们称这样的图形为“L图形”，记作“L图形ABCDEF”．若直线将L图形分成面积相等的两个图形，则称这样的直线为该L图形的面积平分线．
【活动】
小华同学给出了图1的面积平分线的一个作图方案：如图2，将这个L图形分成矩形AGEF、矩形GBCD，这两个矩形的对称中心O1，O2所在直线是该L图形的面积平分线．
请用无刻度的直尺在图1中作出其他的面积平分线．（作出一种即可，不写作法，保留作图痕迹）
【思考】
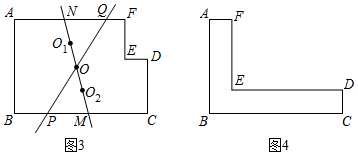
如图3，直线O1O2是小华作的面积平分线，它与边BC，AF分别交于点M，N，过MN的中点O的直线分别交边BC，AF于点P，Q，直线PQ 是是（填“是”或“不是”）L图形ABCDEF的面积平分线．
【应用】
在L图形ABCDEF形中，已知AB=4，BC=6．
（1）如图4，CD=AF=1．
①该L图形的面积平分线与两条水平的边分别相交于点P，Q，求PQ长的最大值；
②该L图形的面积平分线与边AB，CD分别相交于点G，H，当GH的长取最小值时，BG的长为 3434．
（2）设CDAF=t（t＞0），在所有的与铅直方向的两条边相交的面积平分线中，如果只有与边AB，CD相交的面积平分线，直接写出t的取值范围 t＞23t＞23．
3
4
3
4
CD
AF
2
3
2
3
【考点】四边形综合题．
【答案】是；；t＞
3
4
2
3
【解答】
【点评】
声明：本试题解析著作权属菁优网所有，未经书面同意，不得复制发布。
发布：2024/9/7 9:0:8组卷：1736引用：2难度：0.1
相似题
-
1．如图所示，将矩形OABC置于平面直角坐标系中，点A，C分别在x,y轴的正半轴上，已知点B（4，2），将矩形OABC翻折，使得点C的对应点P恰好落在线段OA（包括端点O，A）上，折痕所在直线分别交BC、OA于点D、E；若点P在线段OA上运动时，过点P作OA的垂线交折痕所在直线于点Q．
（1）求证：CQ=QP
（2）设点Q的坐标为（x,y），求y关于x的函数关系式及自变量x的取值范围；
（3）如图2，连接OQ，OB，当点P在线段OA上运动时，设三角形OBQ的面积为S，当x取何值时，S取得最小值，并求出最小值；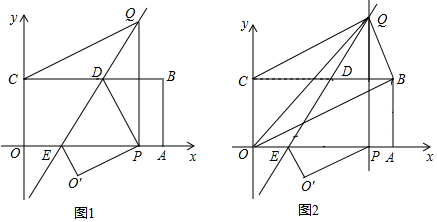
发布：2025/6/9 23:0:1组卷：175引用：3难度：0.1 -
2．在数学兴趣小组活动中，小明进行数学探究活动．将边长为2的正方形ABCD与边长为3的正方形AEFG按图1位置放置，AD与AE在同一条直线上，AB与AG在同一条直线上．
（1）小明发现DG=BE且DG⊥BE，请你给出证明．
（2）如图2，小明将正方形ABCD绕点A逆时针旋转，当点B恰好落在线段DG上时，请你帮他求出此时△ADG的面积．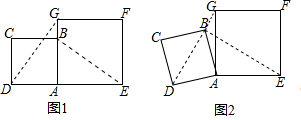
发布：2025/6/9 22:0:2组卷：408引用：8难度：0.3 -
3．（1）问题背景
如图甲，∠ADC=∠B=90°，DE⊥AB，垂足为E，且AD=CD，DE=5，求四边形ABCD的面积．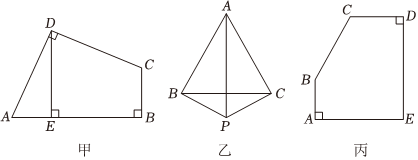
请直接写出四边形ABCD的面积为 ．
小明发现四边形ABCD的一组邻边AD=CD，这就为旋转作了铺垫．于是，小明同学有如下思考过程：
第一步：将△ADE绕点D逆时针旋转90°；
第二步：利用∠A与∠DCB互补，
证明F、C、B三点共线，
从而得到正方形DEBF；
进而求得四边形ABCD的面积．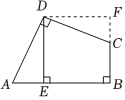
（2）类比迁移
如图乙，P为等边△ABC外一点，BP=1，CP=3，且∠BPC=120°，求四边形ABPC的面积．
（3）拓展延伸
如图丙，在五边形ABCDE中，BC=4，CD+AB=4，AE=DE=6，AE⊥AB，DE⊥CD，求五边形ABCDE的面积．发布：2025/6/9 22:30:2组卷：850引用：6难度：0.3
