阅读理解：若A、B、C为数轴上三点，若点C到A的距离是点C到B的距离2倍，我们就称点C是【A，B】的好点．
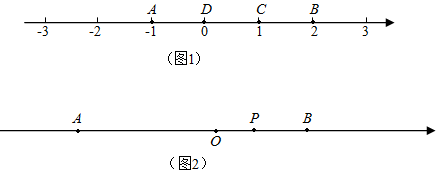
例如，如图1，点A表示的数为-1，点B表示的数为2．表示1的点C到点A的距离是2，到点B的距离是1，那么点C是【A，B】的好点；
又如，表示0的点D到点A的距离是1，到点B的距离是2，那么点D就不是【A，B】的好点，但点D是【B，A】的好点．
知识运用：（1）如图1，点B是【D，C】的好点吗？是是（填是或不是）；
（2）如图2，A、B为数轴上两点，点A所表示的数为-402，点B所表示的数为202．现有一只电子蚂蚁P从点B出发，以22个单位每秒的速度向左运动，到达点A停止．设运动时间为t秒，当t为何值时，P、A和B中恰有一个点为其余两点的好点？
-
40
2
20
2
2
2
【答案】是
【解答】
【点评】
声明：本试题解析著作权属菁优网所有，未经书面同意，不得复制发布。
发布：2024/10/23 7:0:1组卷：67引用：3难度：0.6
相似题
-
1．某钢材加工厂生产甲、乙两种型号的商品，商品的体积和质量分别如表所示：
（1）已知一批商品包含甲、乙两种型号，体积共26m3，质量共14吨，求甲、乙两种型号的商品各有几件？体积（m3/件） 质量（吨/件） 甲种商品 0.8 0.5 乙种商品 2 1
（2）物流公司现有可供使用的货车每辆额定载重3.5吨，容积为6m3，收费方式有以下两种：
①按车收费：每辆车运输货物到目的地收费600元；
②按吨收费：每吨货物运输到目的地收费250元．
要将（1）中的商品一次或分批运输到目的地，该公司应如何选择运送付费方式，能够使得运费最少？并求出该方式下的运费是多少元？发布：2025/6/7 15:30:1组卷：30引用：1难度：0.5 -
2．如图是一根可伸缩的钓鱼竿，它是用10节大小不同的空心套管连接而成．闲置时鱼竿可收缩，完全收缩后，鱼竿长度即为第1节套管的长度（如图1所示）：使用时，可将鱼竿的每一节套管都完全拉伸（如图2所示）．图3是这根鱼竿所有套管都处于完全拉伸状态下的平面示意图．已知第1节套管长50cm,第2节套管长46cm,以此类推，每一节套管均比前一节套管少4cm,完全拉伸时，为了使相邻两节套管连接并固定，每相邻两节套管间均有相同长度的重叠，设其长度为x cm.
（1）请直接写出第3节套管的长度；
（2）请直接用含n的式子表示第n节套管的长度（1≤n≤10）；
（3）当这根鱼竿完全拉伸时，其长度为311cm,求x的值．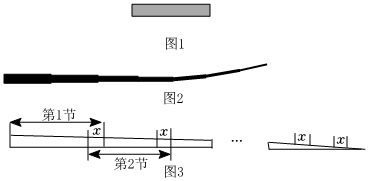
发布：2025/6/7 14:0:1组卷：76引用：1难度：0.5 -
3．在“节粮减损，XX学校在行动”的活动中，A老师带领七年级两个班学生分组进行食堂相关数据采集活动．原计划每个小组分8个学生，刚好分完；后重新编组，每组分12个学生，刚好比原计划少2个组．请问七年级1、2班共有学生多少人？
发布：2025/6/7 17:30:1组卷：11引用：1难度：0.7
