∠MOQ=90°，点A，B分别在射线OM、OQ上运动（不与点O重合）．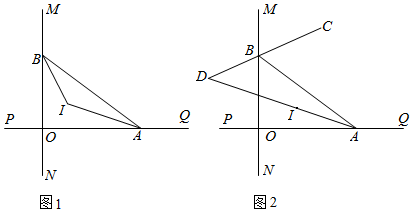
（1）如图1，AI平分∠BAO，BI平分∠ABO，若∠BAO=40°，求∠AIB的度数．
（2）如图2，AI平分∠BAO，BC平分∠ABM，BC的反向延长线交AI于点D．
①若∠BAO=40°，则∠ADB=4545°；
②点A、B在运动的过程中，∠ADB是否发生变化，若不变，试求∠ADB的度数；若变化，请说明变化规律．
【考点】三角形内角和定理．
【答案】45
【解答】
【点评】
声明：本试题解析著作权属菁优网所有，未经书面同意，不得复制发布。
发布：2024/10/16 6:0:3组卷：1308引用：6难度：0.5
相似题
-
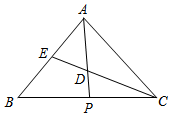1．如图，点D是△ABC两条角平分线AP、CE的交点，如果∠BAC+∠BCA=130°，那么∠ADC=°．发布：2025/6/20 0:30:1组卷：19引用：1难度：0.7 -
2．如图，在△ABC中，AE，CD分别是∠BAC，∠ACB的平分线，且AE，CD相交于点F．
（1）若∠BAC=80°，∠ACB=40°，求∠AFC的度数；
（2）若∠B=80°，求∠AFC的度数；
（3）若∠B=x°，用含x的代数式表示∠AFC的度数．发布：2025/6/19 23:0:1组卷：491引用：7难度：0.5 -
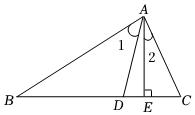3．如图，在△ABC中，AD平分∠BAC．AE⊥BC，∠B=44°，∠DAE=18°，则∠2=°发布：2025/6/20 0:0:1组卷：9引用：1难度：0.6
