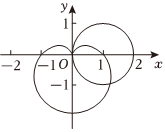
如图，在平面直角坐标系xOy中，以坐标原点为极点，极轴所在的直线为x轴建立极坐标系，曲线C₁是经过极点且圆心在极轴上的直径为2的圆，曲线C₂是著名的笛卡尔心形曲线，它的极坐标方程为ρ=1-sinθ（θ∈[0，2π]）．
（1）求曲线C₁的极坐标方程，并求曲线C₁和曲线C₂的交点（异于极点）的极径；
（2）若曲线C₃的参数方程为
x
=
tcos
π
6
y
=
tsin
π
6
（t为参数），且曲线C₃和曲线C₂相交于除极点以外的M，N两点，求线段MN的长度．

【答案】（1）

；（2）2．

【解答】

【点评】

声明：本试题解析著作权属菁优网所有，未经书面同意，不得复制发布。

发布：2024/7/31 8:0:9组卷：18引用：1难度：0.5

相似题

1．在直角坐标系xOy中，以坐标原点为极点，x轴正半轴为极轴建立极坐标系，曲线C₁：ρcosθ=3，曲线C₂：ρ=4cosθ（
0
≤
θ
＜
π
2
）．
（1）求C₁与C₂交点的极坐标；
（2）设点Q在C₂上，
OQ
=
2
3
QP
，求动点P的极坐标方程．
发布：2024/12/29 3:0:1组卷：144引用：5难度：0.3
解析
2．已知点的极坐标是
（
3
，
π
4
）
，则它的直角坐标是

．
发布：2024/12/29 12:30:1组卷：12引用：2难度：0.7
解析
3．极坐标方程ρcosθ=2sin2θ表示的曲线为（　　）
A．一条射线和一个圆 B．一条直线和一个圆
C．两条直线 D．一个圆
发布：2024/12/29 2:30:1组卷：244引用：6难度：0.7
解析

A．一条射线和一个圆	B．一条直线和一个圆
C．两条直线	D．一个圆

1．在直角坐标系xOy中，以坐标原点为极点，x轴正半轴为极轴建立极坐标系，曲线C1：ρcosθ=3，曲线C2：ρ=4cosθ（0≤θ＜π2）．（1）求C1与C2交点的极坐标；（2）设点Q在C2上，OQ=23QP，求动点P的极坐标方程．