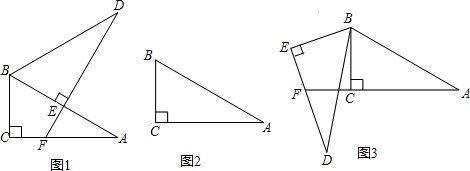
将两个全等的直角三角形ABC和DBE按图①方式摆放，其中∠ACB=∠DEB=90°，∠A=∠D=30°，点E落在AB上，DE所在直线交AC所在直线于点F．
（1）求证：AF+EF=DE；
（2）若将图①中的△DBE绕点B按顺时针方向旋转角α，且0°＜α＜60°，其它条件不变，请在图②中画出变换后的图形，并直接写出你在（1）中猜想的结论是否仍然成立；
（3）若将图①中的△DBE绕点B按顺时针方向旋转角β，且60°＜β＜180°，其它条件不变，如图③．你认为（1）中猜想的结论还成立吗？若成立，写出证明过程；若不成立，请写出AF、EF与DE之间的关系，并说明理由．
【考点】全等三角形的判定与性质．
【答案】见试题解答内容
【解答】
【点评】
声明：本试题解析著作权属菁优网所有，未经书面同意，不得复制发布。
发布：2024/9/11 5:0:9组卷：14231引用：60难度：0.3
相似题
-
1．如图，△ABC的两条高AD和CE交于点F．已知AB=7，EF=EB=3，则CF的长为（ ）发布：2025/6/12 19:0:1组卷：75引用：2难度：0.7 -
2．如图，E、F在线段AC上，∠A=∠C，AE=CF，若∠B=∠D．
求证：DF=BE．发布：2025/6/12 19:0:1组卷：373引用：7难度：0.7 -
3．老师在黑板上画出如图所示的图形（其中点B，F，C，E在同一直线上），并给出四个条件：①AB=DE；②BF=EC；③∠B=∠E；④∠1=∠2，要求同学们从中选出三个作为已知，另一个作为结论来构造一道证明题．甲、乙、丙三位同学的答案如下，则（ ）
甲：①②③→④；乙：②③④→①；丙：①②④→③发布：2025/6/12 19:0:1组卷：4引用：5难度：0.7
