综合与实践
某数学活动小组在一次综合与实践中，对图形平移问题进行了下列探究：问题情境：
如图，一张矩形纸板记为ABCD，AB=5，BC=12，将此矩形纸板沿对角线BD剪开，得到两个全等的直角三角形记为△ABD与△BCD．固定△BCD，将△ABD沿BD方向平移，平移后的三角形记为△A'B'D'，且点B′在对角线BD上．探究发现：
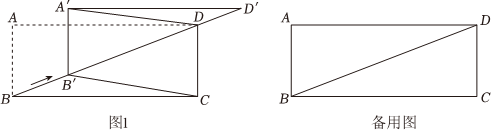
（1）连接A′D，B′C，请判断四边形A′B′CD的形状，并说明理由；
（2）请利用备用图求当△ABD平移到使四边形A′B′CD为菱形时，平移的距离：
（3）在（2）的条件下，不再添加字母，利用已有顶点再构造一个菱形，在备用图上画出图形并直接写出这个菱形的名称；（不需证明）
（4）在△A′B'D'运动过程中，是否存在以点B，B'，C为顶点的三角形是等腰三角形，若存在，请直接写出B'C 的长度；若不存在，请说明理由．
【考点】四边形综合题．
【答案】（1）四边形A′B′CD为平行四边形，理由见解答过程；
（2）平移的距离为；
（3）四边形A′BCD'是菱形；
（4）存在以点B，B'，C为顶点的三角形是等腰三角形，B'C 的长度为12或或．
（2）平移的距离为
119
13
（3）四边形A′BCD'是菱形；
（4）存在以点B，B'，C为顶点的三角形是等腰三角形，B'C 的长度为12或
13
2
12
26
13
【解答】
【点评】
声明：本试题解析著作权属菁优网所有，未经书面同意，不得复制发布。
发布：2024/6/22 8:0:10组卷：43引用：1难度：0.5
相似题
-
1．如图，在四边形ABCD中，∠ABC=∠DCB，点E为BC上一点，且DE∥AB，过点B作BF∥AD交DE的延长线于点F，连接CF，CF=BF．
（1）求证：△ADE≌△FCD；
（2）如图（2），连接DB交AE于点G．
①若AG=DC．求证：BC平分∠DBF；
②若DB∥CF，求的值．CFBD
发布：2025/5/24 5:30:2组卷：3743引用：9难度：0.1 -
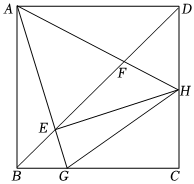2．如图，在正方形ABCD中，点G为BC边上的动点，点H为CD边上的动点，且满足BG+DH=HG，连接AH，AG分别交正方形ABCD的对角线BD于F，E两点，则下列结论中正确的有 .（填序号即可）
①∠DHA=∠GHA；②AF•AH=AE•AG；③BE+DF=EF；④AH=AE2发布：2025/5/24 5:30:2组卷：250引用：1难度：0.3 -
3．等腰Rt△BEF中，∠BEF=90°，BE=EF，先将△BEF绕正方形ABCD的顶点B旋转，再平移线段BE至AG位置，连接DF，GF．
（1）如图1，当点E落在BC上时，直接写出DF、GF的数量关系．
（2）如图2，当点E不在BC上时，（1）中的结论是否依然成立，若成立，请证明，若不成立，请说明理由；
（3）连接AE，若，BE=2，在△BEF绕点B旋转的过程中，当A、G、F三点共线时，直接写出线段AE的长度．AB=25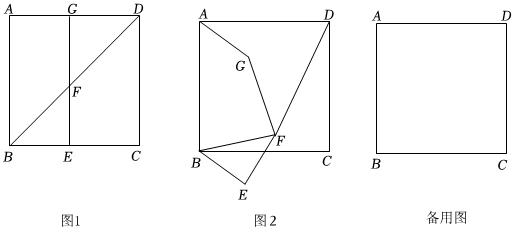
发布：2025/5/24 5:30:2组卷：272引用：2难度：0.2
