已知函数f（x）=exx-lnx+x
（1）讨论函数f（x）的单调性；
（2）若不等式g（x）=x2•f（x）+（x2-1）lnx-x3-x≤t有解，求实数t的取值范围；
（3）若函数h（x）=f（x）-a（a∈R）有两个零点x1，x2，证明：x1•x2＜1．
e
x
x
【考点】利用导数研究函数的单调性；利用导数研究函数的最值．
【答案】（1）在（0，1）上单调递减，在（1，+∞）上单调递增；
（2）取值范围为[1，+∞）；
（3）证明过程见解析．
（2）取值范围为[1，+∞）；
（3）证明过程见解析．
【解答】
【点评】
声明：本试题解析著作权属菁优网所有，未经书面同意，不得复制发布。
发布：2024/8/26 3:0:8组卷：124引用：3难度：0.5
相似题
-
1．已知函数f（x）=x3-2kx2+x-3在R上不单调，则k的取值范围是 ；
发布：2024/12/29 13:0:1组卷：236引用：3难度：0.8 -
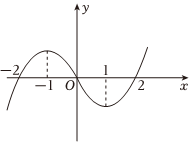2．在R上可导的函数f（x）的图象如图示，f′（x）为函数f（x）的导数，则关于x的不等式x•f′（x）＜0的解集为（ ）发布：2024/12/29 13:0:1组卷：265引用：7难度：0.9 -
3．已知函数f（x）=ax2+x-xlnx（a∈R）
（Ⅰ）若函数f（x）在（0，+∞）上单调递增，求实数a的取值范围；
（Ⅱ）若函数f（x）有两个极值点x1，x2（x1≠x2），证明：．x1•x2＞e2发布：2024/12/29 13:30:1组卷：141引用：2难度：0.2
