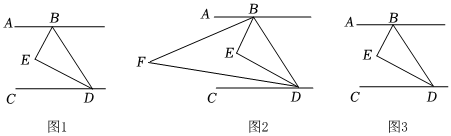
已知BE平分∠ABD，DE平分∠BDC，且∠BED=∠ABE+∠EDC．
（1）如图1，求证：AB∥CD；
（2）如图2，若∠ABE=3∠ABF，且∠BFD=30°时，试求∠CDF∠FDE的值；
（3）如图3，若H是直线CD上一动点（不与D重合），BI平分∠HBD，画出图形，并探究出∠EBI与∠BHD的数量关系．
∠
CDF
∠
FDE
【考点】平行线的判定与性质．
【答案】见试题解答内容
【解答】
【点评】
声明：本试题解析著作权属菁优网所有，未经书面同意，不得复制发布。
发布：2024/10/19 9:0:1组卷：1850引用：5难度：0.4
相似题
-
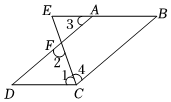1．补全下列推理过程：已知：如图，CE平分∠BCD，∠1=∠2=70°，∠3=40°，求证：AB∥CD．
证明：∵CE平分∠BCD（ ）
∴∠1=（ ）
∵∠1=∠2=70°（已知）
∴∠1=∠2=∠4=70°（ ）
∴AD∥BC（ ）
∴∠D=180°-=180°-∠1-∠4=40°
∵∠3=40°（已知）
∴=∠3
∴AB∥CD（ ）发布：2025/6/20 12:0:2组卷：33引用：2难度：0.7 -
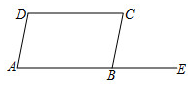2．如图，BE是AB的延长线．
（1）由∠CBE=∠A可以判定哪两条直线平行？根据是什么？
（2）由∠CBE=∠C可以判定哪两条直线平行？根据是什么？发布：2025/6/20 12:0:2组卷：60引用：3难度：0.6 -
3．直线a、b、c在同一平面内，下面的四个结论：
①如果a∥b,a∥c,那么b∥c；
②如果a⊥b,b⊥c,那么a∥c；
③如果a∥b,b⊥c,那么a⊥c；
④如果a与b相交，b与c相交，那么a与c相交；正确的个数为（ ）发布：2025/6/20 12:30:2组卷：589引用：3难度：0.8
