【问题探究】
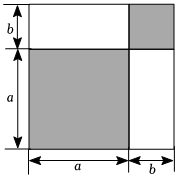
如图，将一个边长为a+b的正方形图形分割成四部分（两个正方形，两个长方形），根据图中条件，请用两种方法表示该图形的总面积，可得如下公式
（a+b）²
（a+b）²
=
a²+2ab+b²
a²+2ab+b²
；
【问题解决】
（1）若a＞b＞0，且满足a²+b²=57，ab=12，a+b=
9
9
；
（2）若（5+x）²+（x+3）²=60，求（5+x）（x+3）的值．

【答案】（a+b）²；a²+2ab+b²；9

【解答】

【点评】

声明：本试题解析著作权属菁优网所有，未经书面同意，不得复制发布。

发布：2024/7/13 8:0:9组卷：271引用：2难度：0.6

相似题

1．把20cm长的一条线段分成两段，将每一段围成一个正方形框，已知两个正方形的面积之差为10cm²，求这两段的长．
发布：2025/6/15 18:30:1组卷：56引用：1难度：0.7
解析
2．如图，将下图中的阴影部分裁剪下来，重新拼成一个如图的长方形．

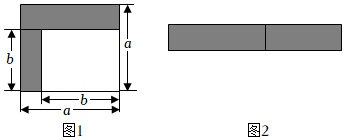
（1）根据两个图中阴影部分的面积相等，可以得到一个乘法公式
，这个公式的名称叫
．
（2）根据你在（1）中得到的公式计算下列算式：
（
1
-
1
2
2
）
（
1
-
1
3
2
）
（
1
-
1
4
2
）
（
1
-
1
5
2
）
…
（
1
-
1
99
2
）
（
1
-
1
100
2
）
．
发布：2025/6/15 17:0:2组卷：87引用：1难度：0.6
解析
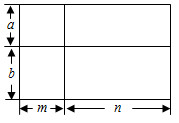3．如图中的四边形均为长方形，根据图形的面积关系，写出一个正确的等式：
．
发布：2025/6/15 9:0:1组卷：317引用：4难度：0.8
解析

1．把20cm长的一条线段分成两段，将每一段围成一个正方形框，已知两个正方形的面积之差为10cm2，求这两段的长．