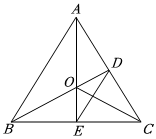
如图，在△ABC中，∠ABC=∠ACB，BD⊥AC于点D，E是BC上一点，连接AE，与BD相交于点O，连接OC，DE，且OB=OC．
（1）求证：AE垂直平分BC；
（2）若∠OED=∠ODE，求证：CO平分∠ACB；
（3）若∠BAC=60°，求证：△CDE是等边三角形．

【答案】证明见解析．

【解答】

【点评】

声明：本试题解析著作权属菁优网所有，未经书面同意，不得复制发布。

发布：2024/7/6 8:0:9组卷：647引用：4难度：0.7

相似题

1．已知：如图，△ABC中，AB=AC，D为BC上一点，过点D作DE∥AB交AC于点E．
（1）求证：∠C=∠CDE．
（2）若∠A=60°，试判断△DEC的形状，并说明理由．
发布：2025/6/22 16:0:1组卷：823引用：6难度：0.7
解析
2．如图，△ABC中，AB=AC，∠BAC=120°，点D、E在边BC上，且BD=AD，CE=AE．判断△ADE的形状，并说明理由．
发布：2025/6/22 19:0:1组卷：60引用：2难度：0.7
解析
3．如图，四边形ABCD中，∠A=∠B，∠C=∠ADC，DE∥BC，且∠ADC-∠A=60°，求证：△ADE是正三角形．
发布：2025/6/22 16:0:1组卷：53引用：2难度：0.6
解析

如图，在△ABC中，∠ABC=∠ACB，BD⊥AC于点D，E是BC上一点，连接AE，与BD相交于点O，连接OC，DE，且OB=OC．（1）求证：AE垂直平分BC；（2）若∠OED=∠ODE，求证：CO平分∠ACB；（3）若∠BAC=60°，求证：△CDE是等边三角形．