综合与实践
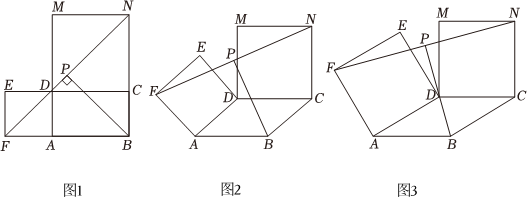
问题情境：数学课上，老师提出如下问题：如图，四边形ABCD是矩形，分别以AD，CD为边，在矩形ABCD外侧作正方形ADEF和CDMN（点B，A，F在同一直线上，点B，C，N在同一直线上）．连接FN，取FN的中点P，连接BP．
求证：BP⊥FN，BP=12FN．
解决问题：
（1）请你解答老师提出的问题．
数学思考：
（2）受到老师所提问题的启发，“兴趣小组”又提出了一个新问题：如图，若四边形ABCD是平行四边形（∠DAB≠90°），其余条件保持不变，则老师所提问题的结论是否保持不变？请你说明理由．
（3）“智慧小组”所提的问题是：如图，四边形ABCD是菱形，分别以AD，CD为边，在菱形外侧作正方形ADEF和CDMN．连接BD并延长，交FN于点P．若∠DAB=30°，FN=6，求BD的长．请你思考该问题，并直接写出结果．
BP
=
1
2
FN
【考点】四边形综合题．
【答案】（1）证明见解析；
（2）不变；
（3）3-．
（2）不变；
（3）3-
3
【解答】
【点评】
声明：本试题解析著作权属菁优网所有，未经书面同意，不得复制发布。
发布：2024/7/27 8:0:9组卷：314引用：2难度：0.4
相似题
-
1．如图，点E，F分别在正方形ABCD的边CD，BC上，且DE=CF，点P在射线BC上（点P不与点F重合）．将线段EP绕点E顺时针旋转90°得到线段EG，过点E作GD的垂线QH，垂足为点H，交射线BC于点Q．
（1）如图1，若点E是CD的中点，点P在线段BF上，
①PQ=；
②线段BP，QC，EC的数量关系为 ．
（2）如图2，若点E不是CD的中点，点P在线段BF上，判断（1）中的结论是否仍然成立，若成立，请写出证明过程；若不成立，请说明理由．
（3）正方形ABCD的边长为9，DE=DC，QC=2，请直接写出线段BP的长．13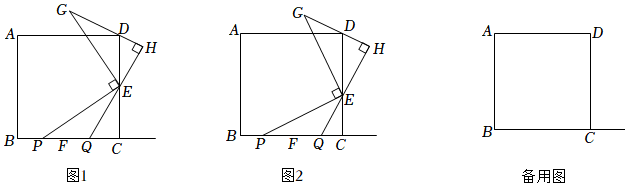
发布：2025/5/25 3:30:2组卷：544引用：4难度：0.4 -
2．如图，四边形ABCD是正方形，E是射线DC上一点，F是CE的中点，将线段EF绕点F逆时针旋转90°得到点GF，连接GE，CG，以CG，CD为邻边作平行四边形CGHD，连接AE，M是AE的中点．
（1）如图1，当点E与点D重合时，HM与AE的位置关系是 ．
（2）如图2，当点E与点D不重合，（1）中的结论是否成立？若成立，请写出证明过程；若不成立，请说明理由；
（3）当DE=2CE时，连接HE，请直接写出tan∠GHE的值．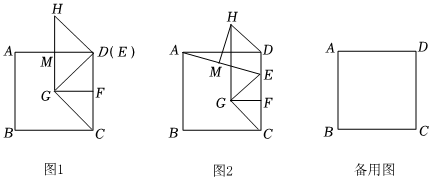
发布：2025/5/25 4:0:1组卷：109引用：1难度：0.1 -
3．在数学兴趣小组活动中，小亮进行数学探究活动．
（1）△ABC是边长为3的等边三角形，E是边AC上的一点，且AE=1，小亮以BE为边作等边三角形BEF，如图1．求CF的长；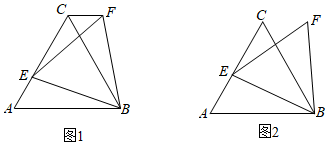
（2）△ABC是边长为3的等边三角形，E是边AC上的一个动点，小亮以BE为边作等边三角形BEF，如图2．在点E从点C到点A的运动过程中，求点F所经过的路径长；
（3）△ABC是边长为3的等边三角形，M是高CD上的一个动点，小亮以BM为边作等边三角形BMN，如图3．在点M从点C到点D的运动过程中，求点N所经过的路径长；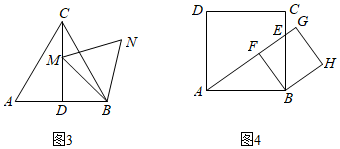
（4）正方形ABCD的边长为3，E是边CB上的一个动点，在点E从点C到点B的运动过程中，小亮以B为顶点作正方形BFGH，其中点F、G都在直线AE上，如图4．当点E到达点B时，点F、G、H与点B重合．则点H所经过的路径长为，点G所经过的路径长为．发布：2025/5/25 2:30:1组卷：3595引用：2难度：0.2
