空间中，两两互相垂直且有公共原点的三条数轴构成直角坐标系，如果坐标系中有两条坐标轴不垂直，那么这样的坐标系称为“斜坐标系”．现有一种空间斜坐标系，它任意两条数轴的夹角均为60°，我们将这种坐标系称为“斜60°坐标系”．我们类比空间直角坐标系，定义“空间斜60°坐标系”下向量的斜60°坐标：i，j，k分别为“斜60°坐标系”下三条数轴（x轴、y轴、z轴）正方向的单位向量，若向量n=xi+yj+zk，则n与有序实数组（x,y,z）相对应，称向量n的斜60°坐标为[x,y,z]，记作n=[x,y,z]．
（1）若a=[1，2，3]，b=[-1，1，2]，求a+b的斜60°坐标；
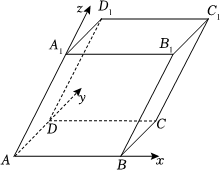
（2）在平行六面体ABCD-ABC1D1中，AB=AD=2，AA1=3，∠BAD=∠BAA1=∠DAA1=60°，如图，以{AB，AD，AA1}为基底建立“空间斜60°坐标系”．
①若BE=EB1，求向量ED1的斜60°坐标；
②若AM=[2，t,0]，且AM⊥AC1，求|AM|．
i
，
j
，
k
n
=
x
i
+
y
j
+
z
k
n
n
n
=
[
x
,
y
,
z
]
a
=
[
1
，
2
，
3
]
b
=
[
-
1
，
1
，
2
]
a
+
b
{
AB
，
AD
，
A
A
1
}
BE
=
EB
1
ED
1
AM
=
[
2
，
t
,
0
]
AM
⊥
A
C
1
|
AM
|
【考点】空间向量单位正交基底及其表示空间向量．
【答案】（1）[0，3，5]
（2）①；②2．
（2）①
[
-
2
，
2
，
3
2
]
【解答】
【点评】
声明：本试题解析著作权属菁优网所有，未经书面同意，不得复制发布。
发布：2024/9/4 17:0:8组卷：116引用：3难度：0.6
相似题
-
1．已知点A在基底{
，a，b}下的坐标为{8，6，4}，其中c，a=i+j，b=j+k，则点A在基底{c=k+i，i，j}下的坐标为（ ）k发布：2024/10/13 6:0:6组卷：86引用：1难度：0.8 -
2．设
，a1=2m-j+k，a2=m+3j-2k，a3=-2m+j-3k，其中a4=3m+2j+5k，m，j是两两垂直的单位向量，若k，则实数λ，μ，v的值分别是（ ）a4=λa1+μa2+va3发布：2024/10/3 5:0:1组卷：75引用：3难度：0.5 -
3．已知向量
是空间中三个两两垂直的单位向量，i，j，k，则m=4j+5k，n=-8i+5j-4k的值为（ ）m•n发布：2024/10/11 2:0:4组卷：70引用：2难度：0.5
