如图1，将三角板放在正方形ABCD上，使三角板的直角顶点E与正方形ABCD的顶点A重合，三角板的一边交CD于点F．另一边交CB的延长线于点G．
（1）求证：EF=EG；
（2）如图2，移动三角板，使顶点E始终在正方形ABCD的对角线AC上，其他条件不变，（1）中的结论是否仍然成立？若成立，请给予证明：若不成立．请说明理由；
（3）如图3，将（2）中的“正方形ABCD”改为“矩形ABCD”，且使三角板的一边经过点B，其他条件不变，若AB=a、BC=b,求EFEG的值．
EF
EG
【答案】见试题解答内容
【解答】
【点评】
声明：本试题解析著作权属菁优网所有，未经书面同意，不得复制发布。
发布：2024/8/23 15:0:9组卷：2724引用：23难度：0.5
相似题
-
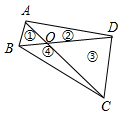1．如图，四边形ABCD的对角线AC、BD相交于O，且将这个四边形分成①、②、③、④四个三角形，若OA：OC=OB：OD，则下列结论中一定正确的是（ ）发布：2025/6/17 5:0:1组卷：973引用：7难度：0.6 -
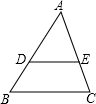2．如图，D、E分别是△ABC的边AB、AC上的点，DE∥BC，=2，那么△ADE与四边形DBCE的面积的比是（ ）ADDB发布：2025/6/17 5:0:1组卷：236引用：26难度：0.7 -
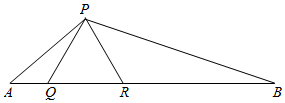3．如图：△PQR是等边三角形，∠APB=120°．
（1）求证：QR2=AQ•RB．
（2）若AP=2，AQ=2．求RQ的长和△PRB的面积．7发布：2025/6/17 5:30:3组卷：199引用：1难度：0.4
