如图1，AB为⊙O的直径，点C、D在⊙O上，弧AD=弧BD，连接AC、CD．
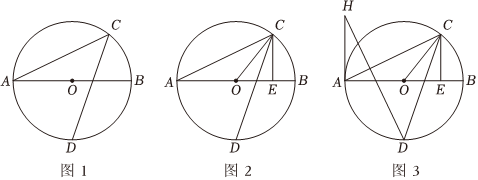
（1）求∠ACD的度数；
（2）如图2，连接OC，过点C作CE⊥AB，垂足为E，求证：CD平分∠OCE；
（3）如图3，在（2）的条件下，AH为⊙O的切线，连接DH，AC⊥DH，tan∠H=12，BE=2，求⊙O的半径．
1
2
【考点】圆的综合题．
【答案】（1）45°；
（2）证明见解析过程；
（3）5．
（2）证明见解析过程；
（3）5．
【解答】
【点评】
声明：本试题解析著作权属菁优网所有，未经书面同意，不得复制发布。
发布：2024/10/22 10:0:2组卷：32引用：2难度：0.1
相似题
-
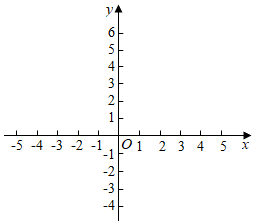1．在平面直角坐标系xOy中，A，B两点的坐标分别为（2，2），B（2，-2），对于给定的线段AB及点P，Q，给出如下定义：若点Q关于AB所在直线的对称点Q，落在△ABP的内部（不含边界），则称点Q是点P关于线段AB的内称点．
（1）已知点P（4，-1）．
①在Q1（1，-1），Q2（1，1）两点中，是点P关于线段AB的内称点的是；
②若点M在直线y=x-1上，且点M是点P关于线段AB的内称点，求点M的横坐标xM的取值范围；
（2）已知点C（3，3），OC的半径为r,点D（4，0），若点E是点D关于线段AB的内称点，且满足直线DE与⊙C相切，求半径r的取值范围．发布：2025/6/20 1:0:2组卷：52引用：2难度：0.3 -
2．对平面内的∠AOB和一点P，如果在∠AOB的边OA和OB上分别存在点M和点N（点M与点N可以重合），满足PM=PN=1，则称点P是∠AOB的“聚点”．若P1和P2是∠AOB的任意两个不同的聚点，把线段P1P2的最大长度称为∠AOB的“轴距”，简记为d（∠AOB）．已知点A（4，0），点B（n,3）．
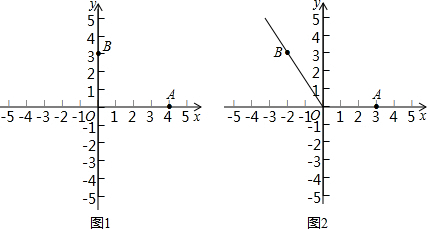
（1）如图1，当n=0时，在点P1（1，2），P2（-1，0），P3（-1，1），P4（-，-12）中，∠AOB的聚点有 ；12
（2）当0≤n≤4时，求∠AOB的轴距d（∠AOB）的取值范围；
（3）如图2，当n=-时，点T在∠AOB的平分线OC所在的直线上运动，以T为圆心作半径为2的圆，若⊙T上存在∠AOB的聚点，求点T的横坐标xT的取值范围．3发布：2025/6/20 1:0:2组卷：244引用：3难度：0.3 -
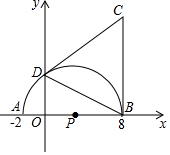3．如图，平面直角坐标系中，A（-2，0），B（8，0），以AB为直径作半圆P交y轴于点D，过点B作BC⊥x轴，且BC=10，连接CD．
（1）图中⊙P的半径长为，点D的坐标为；
（2）求证：直线CD是⊙P的切线；
（3）求tan∠CDB的值．发布：2025/6/18 13:0:8组卷：103引用：1难度：0.5
