某校数学活动小组在一次活动中，对一个数学问题作如下探究：
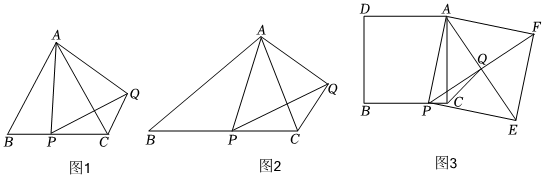
（1）问题发现：如图1，在等边△ABC中，点P是边BC上任意一点，连接AP，以AP为边作等边△APQ，连接CQ．求证：BP=CQ．
（2）变式探究：如图2，在等腰△ABC中，AB=BC，点P是边BC上任意一点，以AP为腰作等腰△APQ，使AP=PQ，∠APQ=∠ABC，连接CQ．判断∠ABC和∠ACQ的数量关系，并说明理由．
（3）解决问题：如图3，在正方形ADBC中，点P是边BC上一点，以AP为边作正方形APEF，Q是正方形APEF的中心，连接CQ．若正方形APEF的边长为12，CQ=42，求正方形ADBC的边长．
CQ
=
4
2
【考点】四边形综合题．
【答案】见试题解答内容
【解答】
【点评】
声明：本试题解析著作权属菁优网所有，未经书面同意，不得复制发布。
发布：2024/7/24 8:0:9组卷：483引用：5难度：0.3
相似题
-
1．如图，△ABC中，∠CAB与∠CBA均为锐角，分别以CA、CB为边向△ABC外侧作正方形CADE和正方形CBFG，再作DD1⊥直线AB于D1，FF1⊥直线AB于F1．
（1）如图（1），过点C作CH⊥AB于H，求证：DD1+FF1=AB；
（2）如图（2），连接EG，问△ABC的面积与△ECG的面积是否相等？请说明理由；
（3）如图（3），过点C作CM⊥EG于M，延长MC交AB于点N，求证：AN=BN．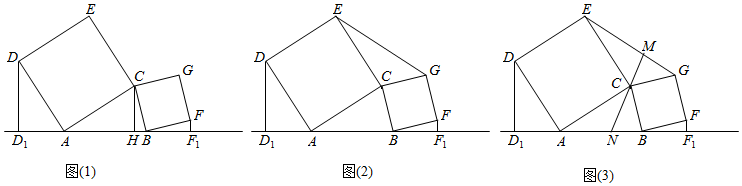
发布：2025/6/21 3:30:1组卷：127引用：3难度：0.5 -
2．如图直角坐标系中直线AB与x轴正半轴、y轴正半轴交于A，B两点，已知B（0，4），∠BAO=30°，P，Q分别是线段OB，AB上的两个动点，P从O出发以每秒3个单位长度的速度向终点B运动，Q从B出发以每秒8个单位长度的速度向终点A运动，两点同时出发，当其中一点到达终点时整个运动结束，设运动时间为t（秒）．
（1）求线段AB的长，及点A的坐标；
（2）t为何值时，△BPQ的面积为2；3
（3）若C为OA的中点，连接QC，QP，以QC，QP为邻边作平行四边形PQCD，
①t为何值时，点D恰好落在坐标轴上；
②是否存在时间t使x轴恰好将平行四边形PQCD的面积分成1：3的两部分，若存在，直接写出t的值．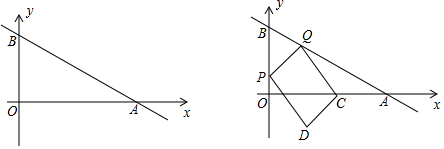
发布：2025/6/20 23:0:1组卷：1027引用：6难度：0.3 -
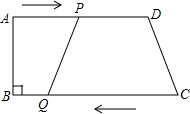3．如图，在梯形ABCD中，AD∥BC，∠B=90°，AB=10cm,AD=20cm,BC=24cm,动点P从点A出发沿AD方向向点D以1cm/s的速度运动，动点Q从点C开始沿CB方向向点B以3cm/s的速度运动．P、Q两点同时出发，设运动时间为t,当其中一点到达端点时，另一点随之停止运动．
（1）当t=3时，PD=，CQ=．
（2）当t为何值时，四边形CDPQ是平行四边形？请说明理由．
（3）在运动过程中，设四边形CDPQ的面积为S，写出S与t的函数关系式，并求当t为何值时，S的值最大，最大值是多少？发布：2025/6/21 2:0:1组卷：147引用：2难度：0.3
