近几年,电商的蓬勃发展带动了快递行业的迅速增长.为了获得更大的利润,某快递公司在A城市的网点对“一天中收发一件块递的平均成本yi(单位:元)与当天揽收的快递件数xi(单位:千件)之间的关系”进行调查研究,得到相关数据如下表:
| 每天揽收快递件数xi(千件) | 2 | 3 | 4 | 5 | 8 |
| 每件快递的平均成本yi(元) | 5.6 | 4.8 | 4.4 | 4.3 | 4.1 |
̂
y
=
-
0
.
2
x
+
5
.
6
̂
y
=
3
.
5
+
4
x
(1)为了评价两种模型的拟合效果,完成以下问题:
①根据上表数据和相应回归方程,将以下表格坋写完整(结果保留一位小数):
| 每天揽收快递件数xi/千件 | 2 | 3 | 4 | 5 | 8 | |
| 每件快递的平均成本yi/元 | 5.6 | 4.8 | 4.4 | 4.3 | 4.1 | |
| 模型甲 | 预报值 | 5.2 | 5 | 4.8 | ||
| 随机误差 ̂ e i |
-0.4 | 0.2 | 0.4 | |||
| 模型乙 | 预报值 ̂ y i |
5.5 | 4.8 | 4.5 | ||
| 随机误差 ̂ e i |
-0.1 | 0 | 0.1 | |||
̂
e
i
=
̂
y
i
-
y
i
②分别计算模型甲与模型乙的随机误差平方和Q1,Q2并依此判断哪个模型的拟合效果更好.
(2)已知该快递网点每天能揽收的快递件数x(单位:千件)与揽收一件快递的平均价格t(单位:元)之间的关系是
t
=
10
-
x
2
(
0
<
t
<
10
)
①若一天揽收快递6千件,则当天总利润的预报值是多少?
②为使每天获得的总利润最高,该快递网点应该将揽收一件快递的平均价格定为多少?(备注:利润=价格-成本)
【考点】经验回归方程与经验回归直线.
【答案】(1)①过程见解析;
②模型乙的拟合效果较好;
(2)①预报值为17000(元);
②平均价格定为6.75元.
②模型乙的拟合效果较好;
(2)①预报值为17000(元);
②平均价格定为6.75元.
【解答】
【点评】
声明:本试题解析著作权属菁优网所有,未经书面同意,不得复制发布。
发布:2024/6/7 8:0:9组卷:12引用:1难度:0.6
相似题
-
 1.某科研机构为了了解气温对蘑菇产量的影响,随机抽取了某蘑菇种植大棚12月份中5天的日产量y(单位:kg)与该地当日的平均气温x(单位:℃)的数据,得到如图散点图:
1.某科研机构为了了解气温对蘑菇产量的影响,随机抽取了某蘑菇种植大棚12月份中5天的日产量y(单位:kg)与该地当日的平均气温x(单位:℃)的数据,得到如图散点图:
其中A(3,2),B(5,10),C(8,11),D(9,13),E(10,14).
(1)求出y关于x的线性回归方程;
(2)若该地12月份某天的平均气温为6℃,用(1)中所求的回归方程预测该蘑菇种植大棚当日的产量.
附:线性回归直线方程中,̂y=̂bx+̂a,̂b=n∑i=1xiyi-nxyn∑i=1x2i-nx2.̂a=y-̂bx发布:2024/12/29 11:30:2组卷:104引用:3难度:0.7 -
2.两个线性相关变量x与y的统计数据如表:
其回归直线方程是x 9 9.5 10 10.5 11 y 11 10 8 6 5 =̂yx+40,则相应于点(9,11)的残差为 .̂b发布:2024/12/29 12:0:2组卷:115引用:8难度:0.7 -
3.某农科所对冬季昼夜温差(最高温度与最低温度的差)大小与某反季节大豆新品种一天内发芽数之间的关系进行了分析研究,他们分别记录了12月1日至12月6日每天昼夜最高、最低的温度(如图1),以及实验室每天每100颗种子中的发芽数情况(如图2),得到如下资料:
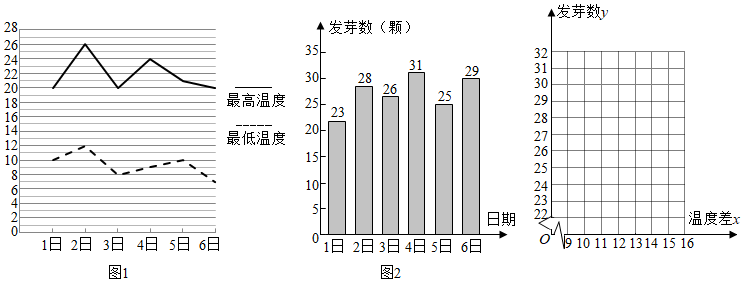
(1)请画出发芽数y与温差x的散点图;
(2)若建立发芽数y与温差x之间的线性回归模型,请用相关系数说明建立模型的合理性;
(3)①求出发芽数y与温差x之间的回归方程(系数精确到0.01);̂y=̂a+̂bx
②若12月7日的昼夜温差为8℃,通过建立的y关于x的回归方程,估计该实验室12月7日当天100颗种子的发芽数.
参考数据:=2051,6∑i=1xi=75,6∑i=1yi=162,6∑i=1xiyi≈4.2,6∑i=1xi2-6x2≈6.5.6∑i=1yi2-6y2
参考公式:
相关系数:r=(当|r|>0.75时,具有较强的相关关系).n∑i=1xiyi-nx•y(n∑i=1xi2-nx2)(n∑i=1yi2-ny2)
回归方程中斜率和截距计算公式:̂y=̂a+̂bx=̂b,n∑i=1xiyi-nx•yn∑i=1xi2-nx2=̂ay-̂b.x发布:2024/12/29 12:0:2组卷:185引用:5难度:0.5


