请阅读下列材料：
已知：如图（1）在Rt△ABC中，∠BAC=90°，AB=AC，点D、E分别为线段BC上两动点，若∠DAE=45°．探究线段BD、DE、EC三条线段之间的数量关系．小明的思路是：把△AEC绕点A顺时针旋转90°，得到△ABE′，连接E′D，使问题得到解决．请你参考小明的思路探究并解决下列问题：
（1）猜想BD、DE、EC三条线段之间存在的数量关系式，直接写出你的猜想；
（2）当动点E在线段BC上，动点D运动在线段CB延长线上时，如图（2），其它条件不变，（1）中探究的结论是否发生改变？请说明你的猜想并给予证明；
（3）已知：如图（3），等边三角形ABC中，点D、E在边AB上，且∠DCE=30°，请你找出一个条件，使线段DE、AD、EB能构成一个等腰三角形，并求出此时等腰三角形顶角的度数．
【答案】见试题解答内容
【解答】
【点评】
声明：本试题解析著作权属菁优网所有，未经书面同意，不得复制发布。
发布：2024/8/7 8:0:9组卷：3085引用：6难度：0.1
相似题
-
1．在△ABC中，BC=a,AC=b,AB=c,若∠C=90°，如图1，则有a2+b2=c2；若△ABC为锐角三角形，小明猜想：a2+b2＞c2．理由如下：
如图2，过点A作AD⊥CB于点D，设CD=x.
在Rt△ADC中，AD2=b2-x2；
在Rt△ADB中，AD2=c2-（a-x）2．
∴b2-x2=c2-（a-x）2，即a2+b2=c2+2ax.
∵a＞0，x＞0，
∴2ax＞0，
∴a2+b2＞c2．
故当△ABC为锐角三角形时，a2+b2＞c2．
∴小明的猜想是正确的．
请你猜想，当△ABC为钝角三角形时，如图3，a2+b2与c2的大小关系，并证明你猜想的结论．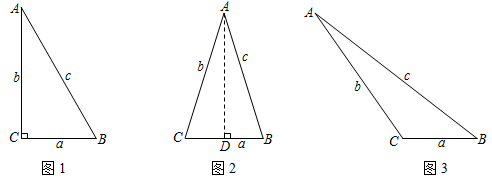
发布：2025/6/17 8:30:1组卷：156引用：1难度：0.5 -
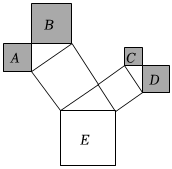2．一株美丽的勾股树如图所示，其中所有的四边形都是正方形，所有的三角形都是直角三角形．若正方形A，B，C，D的面积分别为2，5，1，2，则最大的正方形E的面积是 ．发布：2025/6/17 9:0:1组卷：2438引用：24难度：0.7 -
3．（1）已知两点A（-3，m），B（2m,4），且A和B到x轴距离相等，求B点坐标．
（2）点A在第四象限，当m为何值时，点A（m+2，3m-5）到x轴的距离是它到y轴距离的一半．发布：2025/6/17 8:0:1组卷：44引用：1难度：0.8
