已知点A（0，2），B（0，12），点P为曲线Γ上任意一点且满足|PA|=2|PB|．
（1）求曲线Γ的方程；
（2）设曲线Γ与y轴交于M、N两点，点R是曲线Γ上异于M、N的任意一点，直线MR、NR分别交直线l：y=3于点F、G．求证：以FG为直径的圆C与y轴交于定点S，并求出点S的坐标．
1
2
【考点】曲线与方程．
【答案】（1）x2+y2=1．
（2）当x=0时，由x2+y2=1得y=±1，即M（0，1），N（0，-1），
设点R（x0，y0），（x0≠0），∵点R在曲线Γ上，∴+=1，
直线RM的方程y-1=x，
∴直线RM与直线y=3的交点为F（，3），
直线RN的方程为y+1=x，
∴直线RN与直线y=3的交点为G（，3），
假设存在点S（0，m），使得以FG为直径的圆C与y轴交于定点S，
即•=0成立，
则=（，3-m），=（，3-m），
则•=（，3-m）•（，3-m）=0，
即•+（3-m）2=0
即+（3-m）2=0，
∵+=1，
∴-1=-，
即-8+（3-m）2=0得（m-3）2=8，
得m-3==±2，
解得m=3±2，
∴S点的坐标为（0，3±2）．
（2）当x=0时，由x2+y2=1得y=±1，即M（0，1），N（0，-1），
设点R（x0，y0），（x0≠0），∵点R在曲线Γ上，∴
x
2
0
y
2
0
直线RM的方程y-1=
y
0
-
1
x
0
∴直线RM与直线y=3的交点为F（
2
x
0
y
0
-
1
直线RN的方程为y+1=
y
0
+
1
x
0
∴直线RN与直线y=3的交点为G（
4
x
0
y
0
+
1
假设存在点S（0，m），使得以FG为直径的圆C与y轴交于定点S，
即
SF
SG
则
SF
2
x
0
y
0
-
1
SG
4
x
0
y
0
+
1
则
SF
SG
2
x
0
y
0
-
1
4
x
0
y
0
+
1
即
2
x
0
y
0
-
1
4
x
0
y
0
+
1
即
8
x
2
0
y
2
0
-
1
∵
x
2
0
y
2
0
∴
y
2
0
x
2
0
即-8+（3-m）2=0得（m-3）2=8，
得m-3=
±
8
2
解得m=3±2
2
∴S点的坐标为（0，3±2
2
【解答】
【点评】
声明：本试题解析著作权属菁优网所有，未经书面同意，不得复制发布。
发布：2024/10/25 4:0:2组卷：505引用：2难度：0.5
相似题
-
1．关于曲线C：（x-m）2+（y-m）2=（m-1）2，下列说法正确的是（ ）
发布：2024/12/13 4:0:1组卷：62引用：3难度：0.6 -
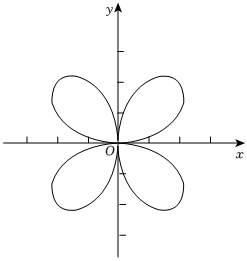2．四叶草曲线是数学中的一种曲线，因形似花瓣，又被称为四叶玫瑰线（如右图），其方程为（x2+y2）3=8x2y2，玫瑰线在几何学、数学、物理学等领域中有广泛应用．例如，它可以用于制作精美的图案、绘制图像、描述物体运动的轨迹等等．根据方程和图象，给出如下4条性质，其中错误的是（ ）发布：2024/12/5 8:30:6组卷：101引用：3难度：0.5 -
3．中国传统文化中很多内容体现了数学中的“对称美”，太极图是由黑白两个鱼形纹组成的圆形图案，充分体现了相互转化、对称统一的形式美、和谐美．定义图象能够将圆O（O为坐标原点）的周长和面积同时等分成两部分的函数称为圆O的一个“太极函数”，给出下列命题：
①对于任意一个圆O，其“太极函数”有无数个；
②函数可以是某个圆O的“太极函数”；f（x）=ln（x2+1-x）
③函数可以同时是无数个圆O的“太极函数”；f（x）=x23
④函数y=f（x）是“太极函数”的充要条件为y=f（x）的图象是中心对称图形．
其中正确结论的序号是（ ）发布：2024/12/17 11:30:2组卷：74引用：2难度：0.6
