阅读问题：已知点A（

1

2

，

3

2

），将OA绕坐标原点逆时针旋转

π

2

至OB，求点B的坐标
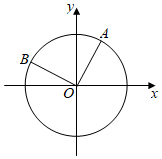
解：如图，点A在角α的终边上，且OA=1，则cosα=

1

2

，sinα=

3

2

，点B在角α+

π

2

的终边上，且OB=1，于是点B的坐标满足：
x_B=cos（

α

+

π

2

）=-sinα=-

3

2

，y_B=sin（

α

+

π

2

）=cosα=

1

2

，即B（-

3

2

，

1

2

）．
（1）将OA绕原点顺时针旋转

π

2

并延长至点C使OC=4OA，求点C坐标；
（2）若将OA绕坐标原点旋转θ并延长至ON，使ON=r•OA（r＞0），求点N的坐标．（用含有r、θ的数学式子表示）
（3）定义P（x₁，y₁），Q（x₂，y₂）的中点为（

x

1

+

x

2

2

，

y

1

+

y

2

2

），将OA逆时针旋转β角，并延长至OD，使OD=2•OA，且DA的中点M也在单位圆上，求cosβ的值．