某商人将进价为每件8元的某种商品按每件10元出售，每天可销出100件．他想采用提高售价的办法来增加利润．经试验，发现这种商品每件每提价1元，每天的销售量就会减少10件．请问每件售价提高多少元时，才能使一天的利润最大？最大利润是多少元？
【考点】二次函数的应用．
【答案】每件售价提高4元时，才能使一天的利润最大，最大利润是360元．
【解答】
【点评】
声明：本试题解析著作权属菁优网所有，未经书面同意，不得复制发布。
发布：2024/8/1 8:0:9组卷：9引用：3难度：0.5
相似题
-
1．某公司经过市场调查，整理出某种商品在某个月的第x天的售价与销量的相关信息如下表：
已知该商品的进价为40元/件，设销售该商品的日销售利润为w元．第x天 售价（元/件） 日销售量（件） 1≤x≤30 x+60 300-10x
（1）求w与x的函数关系式；
（2）问销售该商品第几天时，日销售利润最大？最大日销售利润为多少元？
（3）问在当月有多少天的日销售利润不低于6160元，请直接写出结果．发布：2025/6/11 18:0:1组卷：461引用：3难度：0.6 -
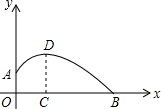2．已知，运动员推铅球经过的路线是抛物线．如图，一个运动员在点A处推出铅球，出手时球离地面约米，在运动员前4米处（即OC=4）达到最高点，高度为3米，铅球在点B处落地．53
（1）求铅球经过抛物线的函数表达式和自变量的取值范围．
（2）求铅球落地点与运动员的距离．发布：2025/6/11 18:0:1组卷：144引用：4难度：0.6 -
3．“武汉加油!中国加油!”疫情牵动万人心，每个人都在为抗击疫情而努力．某厂改造了10条口罩生产线，每条生产线每天可生产口罩500个．如果每增加一条生产线，每条生产线就会比原来少生产20个口罩．设增加x条生产线后，每条生产线每天可生产口罩y个．
（1）直接写出y与x之间的函数关系式；
（2）若每天共生产口罩6000个，在投入人力物力尽可能少的情况下，应该增加几条生产线？
（3）设该厂每天可以生产的口罩w个，请求出w与x的函数关系式，并求出增加多少条生产线时，每天生产的口罩数量最多，最多为多少个？发布：2025/6/11 18:30:2组卷：1960引用：20难度：0.4
