已知▱OABC的边OA在x轴上,点B坐标(8,4)、点C坐标(2,4).点P是x轴正半轴上一个动点,PQ⊥x轴,交边OC或射线CB于点Q,以PQ为底边在其右边作等腰直角△GPQ.
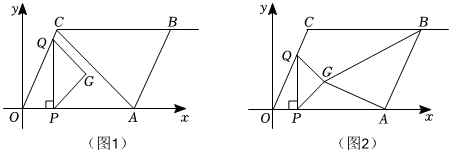
(1)求sin∠CAO的值.
(2)如图1,连结AC,当点G在AC上,证明:点Q与点C重合.
(3)如图2,连结AG、BG,当△ABG是直角三角形时,求点P的坐标.
(4)设△GPQ与▱OABC的重合部分面积为S,令OP=m,当点P从点O运动到点A时,求面积S与m的函数关系式.
【考点】四边形综合题.
【答案】(1);
(2)见解析;
(3)点P的坐标为或或或(10,0);
(4)
.
2
2
(2)见解析;
(3)点P的坐标为
(
3
2
,
0
)
(
5
-
5
,
0
)
(
5
+
5
,
0
)
(4)
S
=
m 2 , 0 ≤ m ≤ 2 |
4 , 2 < m ≤ 5 |
- 4 m 2 + 40 m - 88 3 , 5 < m ≤ 6 |
【解答】
【点评】
声明:本试题解析著作权属菁优网所有,未经书面同意,不得复制发布。
发布:2024/7/2 8:0:9组卷:68引用:2难度:0.1
相似题
-
1.在△ABC中,AB=AC,点D为AB边上一动点,∠CDE=∠BAC=α,CD=ED,连接BE,EC.
(1)问题发现:
如图①,若α=60°,则∠EBA=,AD与EB的数量关系是 ;
(2)类比探究:
如图②,当α=90°时,请写出∠EBA的度数及AD与EB的数量关系并说明理由;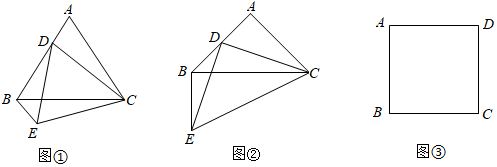
(3)拓展应用:
如图③,点E为正方形ABCD的边AB上的三等分点,以DE为边在DE上方作正方形DEFG,点O为正方形DEFG的中心,若OA=,请直接写出线段EF的长度.2发布:2025/5/25 1:30:1组卷:780引用:3难度:0.3 -
2.背景阅读:
早在三千多年前,我国周朝数学家商高就提出:将一根直尺折成一个直角,如果勾等于三,股等于四,那么弦就等于五,即“勾三、股四、弦五”.它被记载与我国古代著名数学著作《周髀算经》中,为了方便,在本题中,我们把三边的比为3:4:5的三角形称为(3,4,5)型三角形,例如:三边长分别为9,12,15或的三角形就是(3,4,5)型三角形,用矩形纸片按下面的操作方法可以折出这种类型的三角形.32,42,52
实践操作: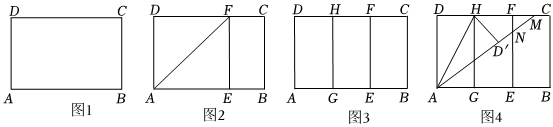
如图1,在矩形纸片ABCD中,AD=8cm,AB=12cm.
第一步:如图2,将图1中的矩形纸片ABCD沿过点A的直线折叠,使点D落在AB上的点E处,折痕为AF,再沿EF折叠,然后把纸片展平.
第二步:如图3,将图2中的矩形纸片再次折叠,使点D与点F重合,折痕为GH,然后展平,隐去AF.
第三步:如图4,将图3中的矩形纸片沿AH折叠,得到△AD′H,再沿AD′折叠,折痕为AM,AM与折痕EF交于点N,然后展平.
问题解决:
(1)请在图4中判断NF与ND′的数量关系,并加以证明;
(2)请在图4中证明△AEN(3,4,5)型三角形;
探索发现:
(3)在不添加字母的情况下,图4中还有哪些三角形是(3,4,5)型三角形?请找出并直接写出它们的名称.发布:2025/5/25 2:0:6组卷:183引用:4难度:0.1 -
3.在数学兴趣小组活动中,小亮进行数学探究活动.
(1)△ABC是边长为3的等边三角形,E是边AC上的一点,且AE=1,小亮以BE为边作等边三角形BEF,如图1.求CF的长;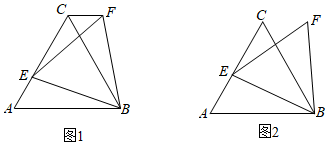
(2)△ABC是边长为3的等边三角形,E是边AC上的一个动点,小亮以BE为边作等边三角形BEF,如图2.在点E从点C到点A的运动过程中,求点F所经过的路径长;
(3)△ABC是边长为3的等边三角形,M是高CD上的一个动点,小亮以BM为边作等边三角形BMN,如图3.在点M从点C到点D的运动过程中,求点N所经过的路径长;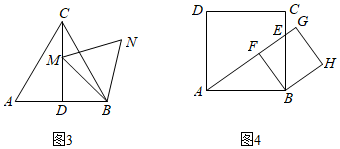
(4)正方形ABCD的边长为3,E是边CB上的一个动点,在点E从点C到点B的运动过程中,小亮以B为顶点作正方形BFGH,其中点F、G都在直线AE上,如图4.当点E到达点B时,点F、G、H与点B重合.则点H所经过的路径长为,点G所经过的路径长为.发布:2025/5/25 2:30:1组卷:3595引用:2难度:0.2


