问题情境：
如图1，△ABC中，BO平分∠ABC，CO平分∠ACD．
（1）探索发现：
若∠A=60°，则∠O的度数为 30°30°；若∠A=130°，则∠O的度数为 65°65°．
（2）猜想证明：
试判断∠A与∠O的关系，并说明理由．
（3）结论应用：
如图2，在四边形MNCB中，BD平分∠MBC，且与四边形MNCB的外角∠NCE的平分线CD交于点D．若∠BMN=130°，∠CNM=100°，则∠D的度数为 25°25°．
【答案】30°；65°；25°
【解答】
【点评】
声明：本试题解析著作权属菁优网所有，未经书面同意，不得复制发布。
发布：2024/7/1 8:0:9组卷：219引用：1难度：0.7
相似题
-
1．如果一个多边形的内角和是360°，那么这个多边形的边数是 ．
发布：2025/6/7 20:0:2组卷：27引用：2难度：0.7 -
2．若一个多边形的外角和与它的内角和相等，则这个多边形的边数是．
发布：2025/6/7 17:0:1组卷：121引用：6难度：0.8 -
3．用两种方法证明“三角形的外角和等于360°”．
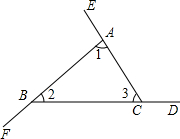
如图，∠BAE、∠CBF、∠ACD是△ABC的三个外角．
求证∠BAE+∠CBF+∠ACD=360°．
证法1：∵，
∴∠BAE+∠1+∠CBF+∠2+∠ACD+∠3=180°×3=540°
∴∠BAE+∠CBF+∠ACD=540°-（∠1+∠2+∠3）．
∵，
∴∠BAE+∠CBF+∠ACD=540°-180°=360°．
请把证法1补充完整，并用不同的方法完成证法2．发布：2025/6/7 17:0:1组卷：295引用：19难度：0.5
