设a∈R，函数f（x）=（a-x）|x|．
（1）若a=1，在直角坐标系中作出函数的图像，并根据图像写出函数的单调区间．
（2）若函数y=f（x+2023）的图象关于点（-2023，0）对称，且对于任意的x∈[-2，2]，不等式mx2+m＞f[f（x）]恒成立，求实数m的范围．
【考点】函数的单调性与函数图象的特征．
【答案】（1）图象见解析，单调递减区间为（-∞，0），；单调递增区间为；
（2）．
（
1
2
，
+
∞
）
（
0
，
1
2
）
（2）
（
16
5
，
+
∞
）
【解答】
【点评】
声明：本试题解析著作权属菁优网所有，未经书面同意，不得复制发布。
发布：2024/10/17 4:0:1组卷：12引用：2难度：0.5
相似题
-
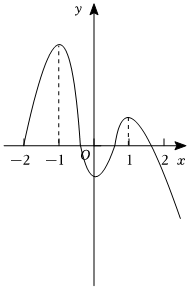1．如图是函数y=f（x）的图象，其定义域为[-2，+∞），则函数f（x）的单调递减区间是（ ）发布：2024/9/21 8:0:8组卷：487引用：6难度：0.7 -
2．设函数f（x）=|ax|+（x+a）（x-a）（a∈R）．
（1）当a=1时，在平面直角坐标系中作出函数f（x）的大致图象，并写出f（x）的单调区间（无需证明）；
（2）若x∈[a,a+1]，求函数f（x）的最小值．发布：2024/6/27 10:35:59组卷：31引用：2难度：0.4 -
3．已知f（x）为R上的偶函数，当x≥0时，f（x）=x2-2x.
（1）求出x＜0时f（x）的解析式，并作出f（x）的图象；
（2）根据图象，写出f（x）的单调区间，并写出（x-1）f（x）＞0的解集．发布：2024/8/6 8:0:9组卷：166引用：2难度：0.8
