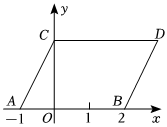
如图，在平面直角坐标系中，点A、B的坐标分别为（-1，0）、（2，0），现同时将点A、B分别向上平移2个单位，再向右平移1个单位，分别得到点A、B的对应点C、D，连接AC、BD、CD．
（1）若在y轴上存在点M，连接MA、MB，使S△MAB=S平行四边形ABDC，求出点M的坐标；
（2）若点P在直线BD上运动，连接PC、PO，若P在线段BD之间时（不与B、D重合），求S△CDP+S△BOP的取值范围；
（3）若点P在第一、四象限，且在直线BD上运动，请直接写出∠CPO、∠DCP、∠BOP的数量关系．
【考点】四边形综合题．
【答案】（1）M（0，4）或（0，-4）；
（2）2＜S△CDP+S△BOP＜3；
（3）∠CPO=∠DCP+∠BOP或∠POB=∠DCP+∠CPO或∠DCP=∠POB+∠CPO．
（2）2＜S△CDP+S△BOP＜3；
（3）∠CPO=∠DCP+∠BOP或∠POB=∠DCP+∠CPO或∠DCP=∠POB+∠CPO．
【解答】
【点评】
声明：本试题解析著作权属菁优网所有，未经书面同意，不得复制发布。
发布：2024/7/20 8:0:8组卷：93引用：1难度：0.1
相似题
-
1．【阅读理解】
（1）如图，已知△ABC中，AB=AC，点D、E是边BC上两动点，且满足∠DAE=∠BAC，12
求证：BD+CE＞DE．
我们把这种模型称为“半角模型”，在解决“半角模型”问题时，旋转是一种常用的方法．
小明的解题思路：将半角∠DAE两边的三角形通过旋转，在一边合并成新的△AFE，然后证明与半角形成的△ADE全等，再通过全等的性质进行等量代换，得到线段之间的数量关系．
请你根据小明的思路写出完整的解答过程．
证明：将△ABD绕点A旋转至△ACF，使AB与AC重合，连接EF，
……
【应用提升】
（2）如图，正方形ABCD（四边相等，四个角都是直角）的边长为4，点P从点A出发，以每秒1个单位长度的速度沿射线AD向点D运动；点Q从点D同时出发，以相同的速度沿射线AD方向向右运动，当点P到达点D时，点Q也停止运动，连接BP，过点P作BP的垂线交过点Q平行于CD的直线l于点E，BE于CD相交于点F，连接PF，设点P运动时间为t（s），
①求∠PBE的度数；
②试探索在运动过程中△PDF的周长是否随时间t的变化而变化？若变化，说明理由；若不变，试求这个定值．发布：2025/6/14 6:0:1组卷：733引用：3难度：0.1 -
2．如图，在▱ABCD中，AC是一条对角线，且AB=AC=5，BC=6，E，F是AD边上两点，点F在点E的右侧，AE=DF，连接CE，CE的延长线与BA的延长线相交于点G．
（1）如图1，M是BC边上一点，连接AM，MF，MF与CE相交于点N．
①若AE=，求AG的长；32
②在满足①的条件下，若EN=NC，求证：AM⊥BC；
（2）如图2，连接GF，H是GF上一点，连接EH．若∠EHG=∠EFG+∠CEF，且HF=2GH，求EF的长．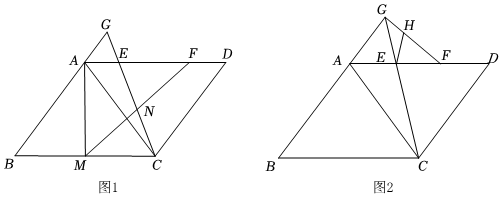
发布：2025/6/14 5:30:3组卷：1288引用：6难度：0.5 -
3．已知：如图，四边形ABCD为矩形，AB=10，BC=3，点E是CD的中点，点P在AB上以每秒2个单位的速度由A向B运动，设运动时间为t秒．
（1）当点P在线段AB上运动了t秒时，BP=（用代数式表示）；
（2）t为何值时，四边形PDEB是平行四边形；
（3）在直线AB上是否存在点Q，使以D、E、Q、P四点为顶点的四边形是菱形？若存在，求出t的值；若不存在，说明理由．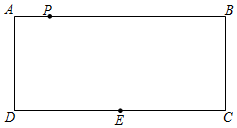
发布：2025/6/14 6:0:1组卷：253引用：6难度：0.2
