已知m2+2mn=384，3mn+2n2=560，那么2m2+13mn+6n2-444的值是
20042004．
【考点】因式分解的应用．
【答案】2004
【解答】
【点评】
声明：本试题解析著作权属菁优网所有，未经书面同意，不得复制发布。
发布：2024/5/27 14:0:0组卷：310引用：2难度：0.7
相似题
-
1．对于一个图形，通过两种不同的方法计算它们的面积，可以得到一个数学等式，例如图1可以得到（a+b）2=a2+2ab+b2，请解答下列问题：
（1）类似图1的数学等式，写出图2表示的数学等式；
（2）若a+b+c=10，ab+ac+bc=35，用上面得到的数学等式乘a2+b2+c2的值；
（3）小明同学用图3中的x张边长为a的正方形，y张边长为b的正方形，z张边长为a、b的长方形拼出一个面积为（a+7b）（9a+4b）的长方形，求（x+y+z）的值．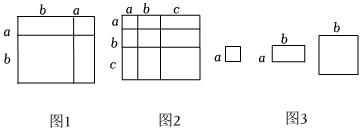
发布：2025/6/7 22:30:2组卷：63引用：2难度：0.6 -
2．利用因式分解进行计算：a（a-b）2-b（b-a）2，其中a=2，
．b=12发布：2025/6/7 22:0:1组卷：23引用：1难度：0.6 -
3．阅读下列材料，并解答下列问题．
材料一：对于实数x、y,我们将x与y的“优雅数”用f（x,y）来表示，定义为f（x,y）=．xy+3
例如f（2，7）=．27+3=210=15
材料二：对于实数x,用[x]表示不超过实数x的最大整数，即满足[x]≤x＜[x]+1．
例如：[-1.3]=[-1.74]=-2，[2]=[2.4]=[2.58]=2．
（1）填空：f（4，5）=，[0]=，[-2.3]=．
（2）已知f（x2-2，4）=2，求x的值．
（3）令t=[-y-1]，若|t|=3，求y的取值范围．23发布：2025/6/7 21:30:1组卷：46引用：2难度：0.5
