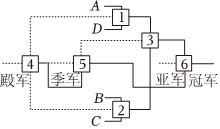
已知某项赛事的季后赛后半段有四支战队参加，采取“双败淘汰赛制”，对阵表如图，赛程如下：
第一轮：四支队伍分别两两对阵（即比赛1和2），两支获胜队伍进入胜者组，两支失败队伍落入败者组．
第二轮：胜者组两支队伍对阵（即比赛3），获胜队伍成为胜者组第一名，失败队伍落入败者组；第一轮落入败者组的两支队伍对阵（即比赛4），失败队伍（已两败）被淘汰（获得殿军），获胜队伍留在败者组．
第三轮：败者组两支队伍对阵（即比赛5），失败队伍被淘汰（获得季军），获胜队伍成为败者组第一名．
第四轮：败者组第一名和胜者组第一名决赛（即比赛6），争夺冠军．
假设每场比赛双方获胜的概率均为0.5，每场比赛之间相互独立．
（1）若第一轮队伍A和队伍D对阵，则他们仍能在决赛中对阵的概率是多少？
（2）已知队伍B在上述季后赛后半段所参加的所有比赛中，败了两场，求在该条件下队伍B获得亚军的概率．