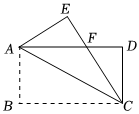
在矩形ABCD中，将△ABC沿AC对折至△AEC位置，CE与AD交于点F．
（1）证明：AF=FC；
（2）如果AB=4，BC=8，求AF的长．

【答案】（1）证明见解答过程；
（2）5．

【解答】

【点评】

声明：本试题解析著作权属菁优网所有，未经书面同意，不得复制发布。

发布：2024/7/9 8:0:8组卷：25引用：2难度：0.5

相似题

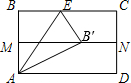1．将矩形ABCD纸对折，设折痕为MN，再把B点叠在折痕线MN上（如图点B′），若AB=
3
，则折痕AE的长为（　　）
A．
3
2
3
B．
3
4
3
C．2 D．2
3
发布：2025/5/28 17:0:2组卷：1031引用：13难度：0.5
解析
2．在△ABC中，已知AB=2a,∠A=30°，CD是AB边的中线，若将△ABC沿CD对折起来，折叠后两个小三角形ACD与三角形BCD重叠部分的面积恰好等于折叠前△ABC的面积的
1
4
，有如下结论：①AC边的长可以等于a；②折叠前的△ABC的面积可以等于
3
2
a
2
；③折叠后，以A、B为端点的线段AB与中线CD平行且相等，其中，正确结论有
个．
发布：2025/5/28 16:0:1组卷：48引用：1难度：0.9
解析
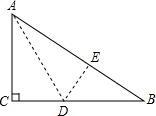3．如图，有一块直角三角形纸片，两直角边AC=6cm,BC=8cm,现将直角边AC沿着直线AD折叠，使它落在斜边AB上，且与AE重合，则CD的长为

cm.
发布：2025/5/28 17:0:2组卷：2104引用：108难度：0.5
解析

在矩形ABCD中，将△ABC沿AC对折至△AEC位置，CE与AD交于点F．（1）证明：AF=FC；（2）如果AB=4，BC=8，求AF的长．