已知：直四棱柱ABCD-A1B1C1D1所有棱长均为2，∠DAB=60°．在该棱柱内放置一个球O，设球O的体积为V1，直四棱柱去掉球O剩余部分的体积为V2．
（1）求三棱锥的A-A1B1D1的表面积S；
（2）求V1V2的最大值．
（只要求写出必要的计算过程，不要求证明）
V
1
V
2
【考点】球的体积和表面积；棱柱、棱锥、棱台的体积．
【答案】见试题解答内容
【解答】
【点评】
声明：本试题解析著作权属菁优网所有，未经书面同意，不得复制发布。
发布：2024/6/27 10:35:59组卷：71引用：3难度：0.6
相似题
-
1．大约于东汉初年成书的我国古代数学名著《九章算术》中，“开立圆术”曰：置积尺数，以十六乘之，九而一，所得开立方除之，即立圆径．“开立圆术”实际是知道了球的体积V，利用球的体积，求其直径d的一个近似值的公式
，而我们知道，若球的半径r,则球的体积d=3169V，则在上述公式V=43πr3中，相当于π的取值为（ ）d=3169V发布：2024/12/30 4:0:3组卷：70引用：2难度：0.6 -
2．正方体的表面积与其外接球的表面积的比为（ ）
发布：2024/12/29 12:30:1组卷：9引用：3难度：0.7 -
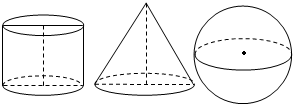3．如图，一个圆柱和一个圆锥的底面直径和它们的高都与一个球的直径2R相等，下列结论正确的是（ ）发布：2024/12/29 9:0:1组卷：332引用：10难度：0.8
