小敏同学有非常良好的学习习惯，在解答人教版数学八（上）教科书P29第8题时，顺利完成后并进行了相应探究，请你经历的思考过程，回答下列问题．
课本真题：如图1，在△ABC中，AD是高，AE是角平分线，∠B=60°，∠C=70°，求∠DAE的度数．
小敏思路：根据∠C的度数先求出∠CAD，有∠B、∠C的度数在求出∠CAE，则结果可得．
（1）请直接写出小敏求出的∠DAE=5°5°．
（2）善于思考的小敏想，∠B、∠C与∠DAE会不会存在固定的数量关系？于是，她试了几组∠B、∠C的度数后（∠C＞∠B），猜想出∠B、∠C与∠DAE的关系为 ∠EAD=12（∠C-∠B）∠EAD=12（∠C-∠B），请证明小敏的猜想；（先填空，再证明）
（3）在（2）的基础上，小敏想到，因为∠DAE与∠AED互余，所以她得出∠B、∠C与∠DAE的关系为2∠AED=180°-（∠C-∠B）．而后，小敏在原图形的基础上作了AE的垂直平分线，交BC的延长线与F点，连接AF，如图2，请你仔细思考，直接写出∠B、∠ACF、∠EAF之间的数量关系 ∠B+∠ACF=2∠EAF∠B+∠ACF=2∠EAF．
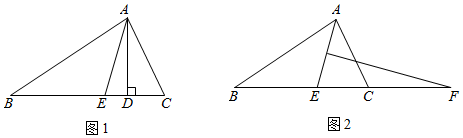
1
2
1
2
【考点】全等三角形的判定与性质；线段垂直平分线的性质．
【答案】5°；∠EAD=（∠C-∠B）；∠B+∠ACF=2∠EAF
1
2
【解答】
【点评】
声明：本试题解析著作权属菁优网所有，未经书面同意，不得复制发布。
发布：2024/8/2 8:0:9组卷：130引用：3难度：0.2
相似题
-
1．如图，△ABC是等边三角形，D为边BC的中点，BE⊥AB交AD的延长线于点E，点F在AE上，且AF=BE，连接CF、CE．
求证：（1）∠CAF=∠CBE；
（2）△CEF是等边三角形．发布：2025/6/9 0:30:2组卷：1096引用：10难度：0.7 -
2．如图，在△ABN和△ACM中，已知AB=AC，AM=AN，∠CAN=∠BAM，求证：∠M=∠N．发布：2025/6/9 0:30:2组卷：47引用：2难度：0.5 -
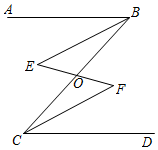3．如图所示，已知AB∥CD，∠ABE=∠DCF，点O是BC的中点，求证：
（1）∠EBO=∠FCO；
（2）BE=CF．发布：2025/6/8 23:30:1组卷：151引用：1难度：0.4
