定义：如果四边形的一条对角线的中点到另外两个顶点的距离都等于这条对角线长的一半，那么我们称这样的四边形为“等距四边形”．
（1）在下列图形中：①平行四边形、②矩形、③菱形，一定是“等距四边形”的是 ②②；（填序号）
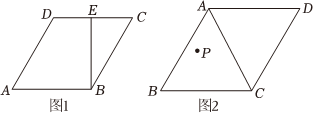
（2）如图1，在菱形ABCD中，AB=4，∠A=60°，BE⊥CD于点E，点F是菱形ABCD边上的一点，顺次连接B、E、D、F，若四边形BEDF为“等距四边形”，求线段EF的长；
（3）如图2，在▱ABCD中，AD=CD=4，AB=AC，点P是△ABC内一点，在AB、BC、CA上是否分别存在点，使得这些点与点P的连线将△ABC恰好分割成三个“等距四边形”，若存在，求这三个“等距四边形”的周长和，若不存在，请说明理由．
【考点】四边形综合题．
【答案】②
【解答】
【点评】
声明：本试题解析著作权属菁优网所有，未经书面同意，不得复制发布。
发布：2024/8/25 16:0:10组卷：44引用：1难度：0.1
相似题
-
1．如图①，平行四边形ABCD的一边DC沿水平方向向右平行移动，图②反映了它的底边BC的长度l（cm）随时间t（s）变化而变化的情况：
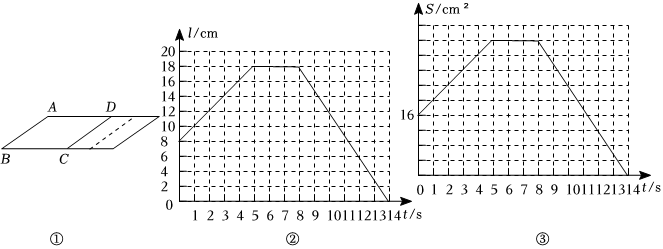（1）边DC没有运动时，底边BC的长度是 cm；
（2）当0＜t≤5时，边DC向右运动的速度为 cm/s,直接写出此时BC的长度l与时间t的关系式 ；
（3）DC边在8s之后运动的方向 ，（填“向左”或“向右”）此时BC的长度l与时间t的关系式 ；
（4）图③反映平行四边形ABCD的面积S（cm2）随时间t（s）变化而变化的情况：平行四边形ABCD中，BC边上的高为 cm,图③中括号填：；
（5）在（4）的条件下，当t=12时，s=cm2，当S=25时，t=s.发布：2025/6/8 9:0:1组卷：186引用：2难度：0.1 -
2．如图，正方形ABCD，AB=4cm,点P在线段BC的延长线上．点P从点C出发，沿BC方向运动，速度为2cm/s；点Q从点A同时出发，沿AB方向运动，速度为1cm/s.连接PQ，PQ分别与BD，CD相交于点E，F．设运动时间为t（s）（0＜t＜4）．解答下列问题：
（1）线段CF长为多少时，点F为线段PQ中点？
（2）当t为何值时，点E在对角线BD中点上？
（3）当PQ中点在∠DCP平分线上时，求t的值；
（4）设四边形BCFE的面积为S（cm2），求S与t的函数关系式．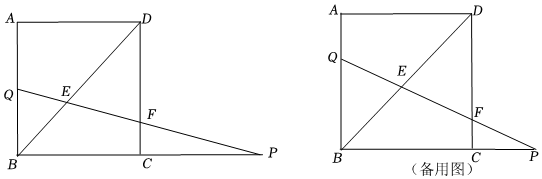
发布：2025/6/8 9:0:1组卷：306引用：2难度：0.1 -
3．综合与实践
问题情境：正方形折叠中的数学
数学活动课上，老师让同学们翻折正方形ABCD进行探究活动，同学们经过动手操作探究，发展了空间观念，并积累了数学活动经验．
问题背景：过点A引射线AH，交边CD于点H（点H与点D不重合），通过翻折，使点B落在射线AH上的点G处，折痕AE交BC于E，延长EG交CD于R如图①．
问题探究：
（1）当点H与点C重合时，FG与FD的大小关系是 ，△CFE是 三角形．
（2）如图②，当点H为边CD上任意一点时（点H与点C不重合），连接AF，猜想FG与FD的数量关系，并说明理由．
问题延伸：
（3）若过点A引直线AH，交直线CD于点H（点H与点D不重合），通过翻折，使点B落在直线AH上的点G处，折痕所在直线AE交直线BC于E，直线EG交直线CD于F连接AF，当AB=5，BE=3时，CF的长为 ．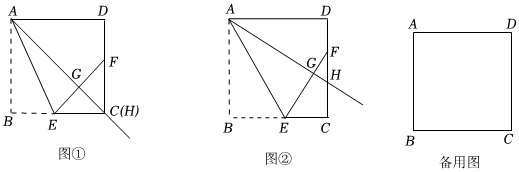
发布：2025/6/8 7:30:1组卷：131引用：2难度：0.2
