学习完平行线的性质与判定之后，我们发现借助构造平行线的方法可以帮我们解决许多问题．
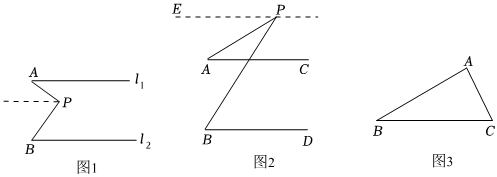
（1）小明遇到了下面的问题：如图1，l1∥l2，点P在l1、l2内部，探究∠A，∠APB，∠B的关系．小明过点P作l1的平行线，可证∠APB，∠A，∠B之间的数量关系是：∠APB=∠A+∠B∠A+∠B．
（2）如图2，若AC∥BD，点P在AC、BD外部，∠A，∠B，∠APB的数量关系是否发生变化？
请你补全下面的证明过程．
解：过点P作PE∥AC．
∴∠A=∠1∠1．
∵AC∥BD，
∴PEPE∥BDBD．
∴∠B=∠BPE∠BPE．
∵∠APB=∠EPB-∠EPA，
∴∠APB=∠B-∠A∠B-∠A．
（3）随着以后的学习你还会发现平行线的许多用途．
试构造平行线解决以下问题：
已知：如图3，三角形ABC，求证：△ABC的内角和是180°．
【考点】三角形综合题．
【答案】∠A+∠B；∠1；PE；BD；∠BPE；∠B-∠A
【解答】
【点评】
声明：本试题解析著作权属菁优网所有，未经书面同意，不得复制发布。
发布：2024/5/9 8:0:9组卷：55引用：1难度：0.2
相似题
-
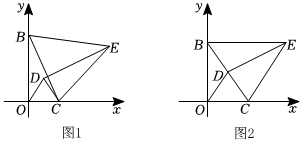
1．如图1，已知点B（0，6），点C为x轴上一动点，连接BC，△ODC和△EBC都是等边三角形．
（1）求证：DE=BO；
（2）如图2，当点D恰好落在BC上时．
①求OC的长及点E的坐标；
②在x轴上是否存在点P，使△PEC为等腰三角形？若存在，写出点P的坐标；若不存在，说明理由．发布：2025/6/9 11:0:1组卷：49引用：1难度：0.5 -
2．感知发现：（1）在学习平行线中，兴趣小组发现了很多有趣的模型图，如图1，当AB∥CD时，可以得到结论：∠BED=∠B+∠D．在学习逆命题时，发现原命题是真命题，逆命题不一定是真命题，于是兴趣小组想尝试证明：如图1，∠BED=∠B+∠D，求证：AB∥CD．请写出证明过程．
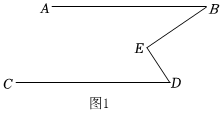
利用这个“模型结论”，我们可以解决很多问题：
综合与实践，（2）在综合与实践课上，同学们以“一个含30°角的直角三角尺和两条平行线”为背景开展数学活动，如图2．已知两直线a,b且a∥b和直角三角形ABC，∠BCA=90°，∠BAC=30°，∠ABC=60°．创新小组的同学发现∠2-∠1=120°，说明理由．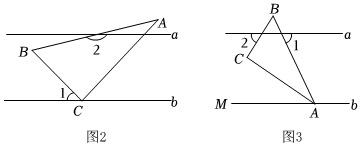
实践探究：（3）缜密小组在创新小组发现结论的基础上，将图2中的图形继续变化得到图3，AC平分∠BAM，此时发现∠1与∠2又存在新的数量关系，请直接写出答案．发布：2025/6/9 11:30:1组卷：317引用：1难度：0.2 -
3．已知AB∥CD，点M、N分别是AB、CD上两点，点G在AB、CD之间，MB．
（1）如图1，若GM⊥GN，求∠AMG+∠CNG的度数：
（2）如图2，若点P是CD下方一点，MG平分∠BMP，ND平分∠GNP，已知∠BMG=32°，求∠MGN+∠MPN的度数；
（3）如图3，若点E是AB上方一点，连接EM、EN，且GM的延长线MF平分∠AME，NE平分∠CNG，2∠MEN+∠MGN=105°，求∠AME的度数．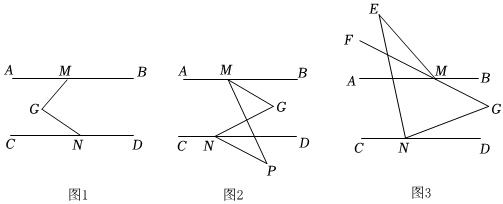
发布：2025/6/9 11:30:1组卷：164引用：1难度：0.3
