小明学习了垂径定理后，做了下面的探究，请根据题目要求帮小明完成探究．
（1）更换定理的题设和结论可以得到许多新的发现．如图1，在⊙O中，C是ˆAB的中点，直线CD⊥AB于点E，则可以得到AE=BE，请证明此结论．
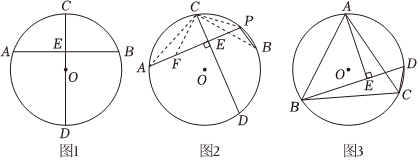
（2）从圆上任意一点出发的两条弦所组成的折线，称为该圆的一条折弦．如图2，古希腊数学家阿基米德发现，若PA、PB是⊙O的折弦，C是ˆAB的中点，CD⊥PA于点E．则AE=PE+PB．这就是著名的“阿基米德折弦定理”．那么如何来证明这个结论呢？小明的证明思路是：在AE上截取AF=PB，连接CA、CF、PC、BC…请你按照小明的思路完成证明过程．
（3）如图3，已知等边三角形ABC内接于⊙O，AB=2，点D是ˆAC上的一点，∠ABD=45°，AE⊥BD于点E，则△BDC的周长为 22+222+2．
ˆ
AB
ˆ
AB
ˆ
AC
2
2
【考点】圆的综合题．
【答案】2+2
2
【解答】
【点评】
声明：本试题解析著作权属菁优网所有，未经书面同意，不得复制发布。
发布：2024/10/16 13:0:2组卷：289引用：2难度：0.3
相似题
-
1．小锐同学是一个数学学习爱好者，他在一本数学课外读物上看到一个课本上没有的与圆相关的角--弦切角（弦切角的定义：把顶点在圆上，一边与圆相切，另一边和圆相交的角叫做弦切角），并尝试用所学的知识研究弦切角的有关性质．
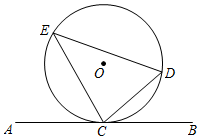
（1）如图，直线AB与⊙O相切于C点，D，E为⊙O上不同于C的两点，连接CE，DE，CD．请你写出图中的两个弦切角 ；（不添加新的字母和线段）
（2）小锐目测∠DCB和∠DEC可能相等，并通过测量的方法验证了他的结论，你能帮小锐用几何推理的方法证明结论的正确性吗？已知：如图，直线AB ，D，E为圆上不同于C的两点，连接CE，DE，CD．求证：．
（3）如果我们把上述结论称为弦切角定理，请你用一句话概括弦切角定理 ．发布：2025/6/16 22:30:4组卷：176引用：2难度：0.5 -
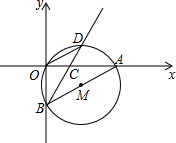2．如图，在直角坐标系中，⊙M经过原点O（0，0），点A（，0）与点B（0，-6），点D在劣弧2上，连接BD交x轴于点C，且∠COD=∠CBO．ˆOA
（1）求⊙M的半径；
（2）求证：BD平分∠ABO；
（3）在线段BD的延长线上找一点E，使得直线AE恰好为⊙M的切线，求此时点E的坐标．发布：2025/6/16 21:30:2组卷：3474引用：15难度：0.1 -
3．如图，直角坐标系中，直线y=kx+b分别交x,y轴于点A（-8，0），B（0，6），C（m,0）是射线AO上一动点，⊙P过B，O，C三点，交直线AB于点D（B，D不重合）．
（1）求直线AB的函数表达式．
（2）若点D在第一象限，且tan∠ODC=，求点D的坐标．53
（3）当△ODC为等腰三角形时，求出所有符合条件的m的值．
（4）点P，Q关于OD成轴对称，当点Q恰好落在直线AB上时，直接写出此时BQ的长．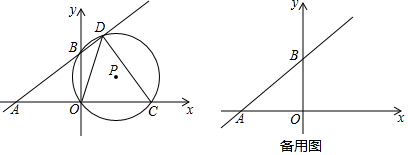
发布：2025/6/16 6:0:1组卷：324引用：5难度：0.1
