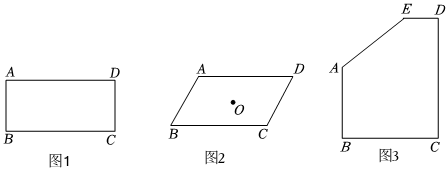
(1)如图1,在矩形ABCD中,AB=4,BC=10,若要在该矩形中作出一个面积最大的△BPC,且使∠BPC=90°,求满足条件的点P到点A的距离.
(2)如图2,有一座古井O,按规定,要以井O为对称中心,建一个面积尽可能大的形状为平行四边形的景区ABCD.根据实际情况,要求顶点A是定点,点A到井O的距离为403米,∠BAD=120°,那么,是否可以建一个满足要求的面积最大的平行四边形景区ABCD?若可以,求出满足要求的平行四边形ABCD的最大面积;若不可以,请说明理由.(井O的占地面积忽略不计)
(3)如图③,有一张五边形卡片ABCDE,小明经过测量得出:AB=25cm,BC=35cm,CD=40cm,∠ABC=∠BCD=∠CDE=90°,∠DEA=150°.小明想在这个五边形卡片ABCDE中裁剪出一个三角形卡片△PAE,使得∠APE=45°,且同时满足三角形卡片△PAE面积最大.请问:小明的想法能否实现?若能,求出△PAE面积的最大值;若不能,请说明理由.(参考数据:2≈1.4.3≈1.7)
3
2
3
【考点】四边形综合题.
【答案】(1)点P到点A的距离2或8.
(2)可以,符合要求的▱BCDE的最大面积为9600m2.
(3)225+225.
(2)可以,符合要求的▱BCDE的最大面积为9600
3
(3)225+225
2
【解答】
【点评】
声明:本试题解析著作权属菁优网所有,未经书面同意,不得复制发布。
发布:2024/10/10 1:0:2组卷:76引用:1难度:0.2
相似题
-
1.如图,在四边形ABCD中,对角线AC,BD相交于点E,已知DB=CB,∠DBC=∠DAC,请认真读图解决下列问题:
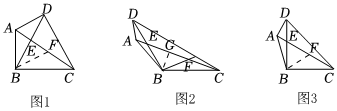
(1)【问题发现】如图1,若∠DBC=∠DAC=60°,写出线段AB,AD,AC之间的数量关系 ;
(2)【类比探究】如图2,若∠DBC=∠DAC=120°,(1)中的结论还成立吗?如不成立,请说明理由;
(3)【拓展延伸】如图3,若∠DBC=∠DAC=90°,AD=1,AB=2,求BC的长.2发布:2025/5/25 9:0:1组卷:79引用:1难度:0.1 -
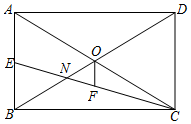 2.如图,在矩形ABCD中,AB=3,AD=4,CE平分∠ACB,与对角线BD相交于点N,F是线段CE的中点,则下列结论中正确的有( )个.
2.如图,在矩形ABCD中,AB=3,AD=4,CE平分∠ACB,与对角线BD相交于点N,F是线段CE的中点,则下列结论中正确的有( )个.
①OF=;②ON=56;③S△CON=2526;④sin∠ACE=1513.513发布:2025/5/25 9:0:1组卷:1188引用:5难度:0.2 -
3.【问题情境】
(1)如图1,在正方形ABCD中,E,F,G分别是BC,AB,CD上的点,FG⊥AE于点Q.求证:AE=FG.
【尝试应用】
(2)如图2,正方形网格中,点A,B,C,D为格点,AB交CD于点O.求tan∠AOC的值;
【拓展提升】
(3)如图3,点P是线段AB上的动点,分别以AP,BP为边在AB的同侧作正方形APCD与正方形PBEF,连接DE分别交线段BC,PC于点M,N.
①求∠DMC的度数;
②连接AC交DE于点H,直接写出的值.DHBC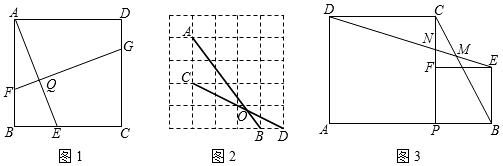 发布:2025/5/25 9:0:1组卷:5569引用:13难度:0.2
发布:2025/5/25 9:0:1组卷:5569引用:13难度:0.2


