在探究完全平方公式：（a±b）2=a2±2ab+b2时，通过适当的变形，可以解决很多数学问题．
例如：若a+b=4，ab=3，求a2+b2的值．
解：因为a+b=4，ab=3，
所以a2+b2=（a+b）2-2ab=42-2×3=10．
请根据上面的解题思路和方法，解决下列问题：
（1）若x-y=10，xy=-22，求x2+y2的值；
（2）将边长为x的正方形ABCD和边长为y的正方形CEFG按如图所示放置，其中点D在边CE上，连接AG，EG，若x+y=14，xy=32，求阴影部分的面积．
【考点】完全平方公式的几何背景．
【答案】（1）56；
（2）50．
（2）50．
【解答】
【点评】
声明：本试题解析著作权属菁优网所有，未经书面同意，不得复制发布。
发布：2024/7/15 8:0:9组卷：251引用：1难度：0.6
相似题
-
1．一个长方形的长减少7cm,宽增加3cm,就成为一个正方形，并且这两个图形的面积相等．则这个长方形的宽为 cm.
发布：2025/6/10 2:0:5组卷：85引用：2难度：0.6 -
2．阅读：若x满足（80-x）（x-60）=30，求（80-x）2+（x-60）2的值．
解：设（80-x）=a,（x-60）=b,则（80-x）（x-60）=ab=30，a+b=（80-x）+（x-60）=20，所以（80-x）2+（x-60）2=a2+b2=（a+b）2-2ab=202-2×30=340．
请仿照上例解决下面的问题：
（1）若x满足（10-x）（x-20）=-10，求（10-x）2+（x-20）2的值；
（2）若x满足（2022-x）2+（2021-x）2=2021，求（2022-x）（2021-x）的值；
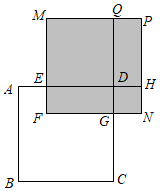
（3）如图，正方形ABCD的边长为x,AE=15，CG=25，长方形EFGD的面积是500，四边形NGDH和MEDQ都是正方形，四边形PQDH是长方形，求图中阴影部分的面积（结果必须是一个具体数值）．发布：2025/6/10 4:0:1组卷：1032引用：3难度：0.4 -
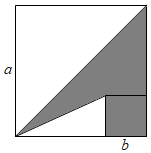3．如图，两个正方形边长分别为a、b,如果a+b=7，ab=10，则阴影部分的面积为（ ）发布：2025/6/10 4:30:1组卷：1014引用：2难度：0.6
