古希腊数学家阿基米德用穷竭法建立了这样的结论：“任何由直线和抛物线所包围的弓形，其面积都是其同底同高的三角形面积的三分之四．”如图，已知直线x=2交抛物线y2=4x于A，B两点，点A，B在y轴上的射影分别为D，C．从长方形ABCD中任取一点，则根据阿基米德这一理论，该点位于阴影部分的概率为（ ）
【考点】几何概型．
【答案】B
【解答】
【点评】
声明：本试题解析著作权属菁优网所有，未经书面同意，不得复制发布。
发布：2024/5/27 14:0:0组卷：50引用：2难度：0.7
相似题
-
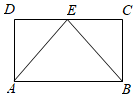1．如图，矩形ABCD中，点E为边CD的中点，若在矩形ABCD内部随机取一个点Q，则点Q取自△ABE内部的概率等于．发布：2025/1/13 8:0:2组卷：30引用：12难度：0.7 -
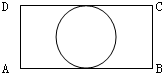2．如图所示，在矩形ABCD中，AB=4cm,BC=2cm,在图形上随机撒一粒黄豆，则黄豆落到圆上的概率是．发布：2025/1/13 8:0:2组卷：9引用：2难度：0.7 -
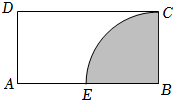3．如图，矩形ABCD，AB=2，BC=1，阴影部分为B为圆心，BC为半径的圆与矩形的重合部分，现在向矩形内随机投掷一点，则该点落在阴影部分以外的概率为（ ）发布：2024/12/29 15:30:4组卷：1引用：1难度：0.7
