如图1，在长方形ABCD中，AB=CD=8cm,AD=BC=10cm,点P从点A出发，沿A→B→C→D的路线运动，到点D停止；点Q从点D出发，沿D→C→B→A的路线运动，到点A停止．若点P，Q同时出发，点P的速度为1cm/s,点Q的速度为3cm/s,运动a秒后，点P，Q同时改变速度，点P的速度变为b cm/s,点Q的速度变为d cm/s,直到停止．图2是点P出发x秒后，△APD的面积S1（cm2）与运动时间x（秒）的关系图象；图3是点Q出发x秒后，△AQD的面积S2（cm2）与运动时间x（秒）的关系图象．
（1）根据图象得：a=66秒，b=44cm/s,c=1111秒，d=11cm/s；
（2）设点P已行的路程为y1（cm），点Q还剩的路程为y2（cm），当x＞a时，请分别求出y1、y2和运动时间x（s）的关系式；
（3）当x=85或5或667或1085或5或667或10时，△PBQ为等腰三角形．
8
5
66
7
8
5
66
7
【考点】四边形综合题．
【答案】6；4；11；1；或5或或10
8
5
66
7
【解答】
【点评】
声明：本试题解析著作权属菁优网所有，未经书面同意，不得复制发布。
发布：2024/6/20 8:0:9组卷：252引用：2难度：0.5
相似题
-
1．如图①，平行四边形ABCD的一边DC沿水平方向向右平行移动，图②反映了它的底边BC的长度l（cm）随时间t（s）变化而变化的情况：
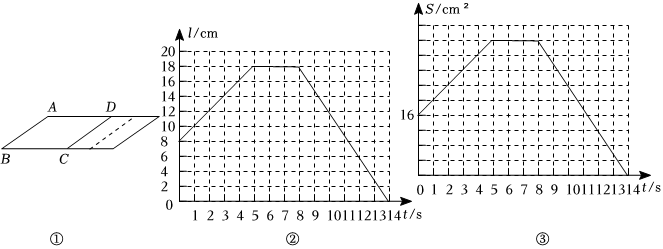（1）边DC没有运动时，底边BC的长度是 cm；
（2）当0＜t≤5时，边DC向右运动的速度为 cm/s,直接写出此时BC的长度l与时间t的关系式 ；
（3）DC边在8s之后运动的方向 ，（填“向左”或“向右”）此时BC的长度l与时间t的关系式 ；
（4）图③反映平行四边形ABCD的面积S（cm2）随时间t（s）变化而变化的情况：平行四边形ABCD中，BC边上的高为 cm,图③中括号填：；
（5）在（4）的条件下，当t=12时，s=cm2，当S=25时，t=s.发布：2025/6/8 9:0:1组卷：186引用：2难度：0.1 -
2．如图，正方形ABCD，AB=4cm,点P在线段BC的延长线上．点P从点C出发，沿BC方向运动，速度为2cm/s；点Q从点A同时出发，沿AB方向运动，速度为1cm/s.连接PQ，PQ分别与BD，CD相交于点E，F．设运动时间为t（s）（0＜t＜4）．解答下列问题：
（1）线段CF长为多少时，点F为线段PQ中点？
（2）当t为何值时，点E在对角线BD中点上？
（3）当PQ中点在∠DCP平分线上时，求t的值；
（4）设四边形BCFE的面积为S（cm2），求S与t的函数关系式．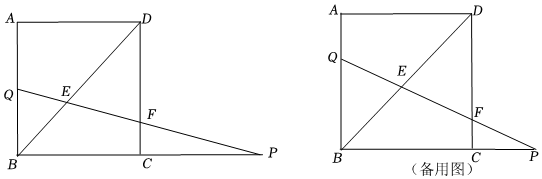
发布：2025/6/8 9:0:1组卷：306引用：2难度：0.1 -
3．综合与实践
问题情境：正方形折叠中的数学
数学活动课上，老师让同学们翻折正方形ABCD进行探究活动，同学们经过动手操作探究，发展了空间观念，并积累了数学活动经验．
问题背景：过点A引射线AH，交边CD于点H（点H与点D不重合），通过翻折，使点B落在射线AH上的点G处，折痕AE交BC于E，延长EG交CD于R如图①．
问题探究：
（1）当点H与点C重合时，FG与FD的大小关系是 ，△CFE是 三角形．
（2）如图②，当点H为边CD上任意一点时（点H与点C不重合），连接AF，猜想FG与FD的数量关系，并说明理由．
问题延伸：
（3）若过点A引直线AH，交直线CD于点H（点H与点D不重合），通过翻折，使点B落在直线AH上的点G处，折痕所在直线AE交直线BC于E，直线EG交直线CD于F连接AF，当AB=5，BE=3时，CF的长为 ．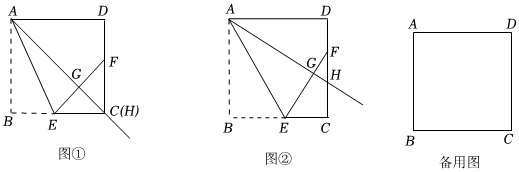
发布：2025/6/8 7:30:1组卷：131引用：2难度：0.2
